Комбинаторика. 99б. Помогите пожалуйста доказать равенство:

Комбинаторика. 99б. Помогите пожалуйста доказать равенство:
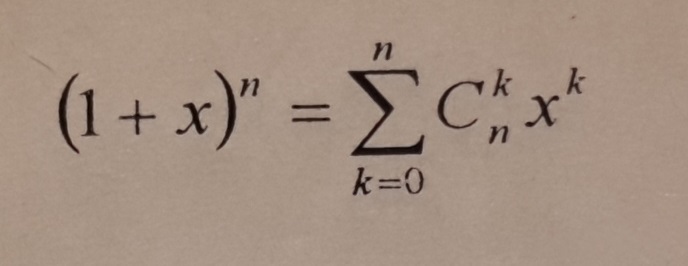
- Предмет:
  Алгебра
- Автор:
  nemesioynne
- 5 лет назад

Ответы 3

Спасибо большущее!
- Автор:
  brandenbradford
- 5 лет назад
- 0
Прочитав такое, просто респект огроменный... Я понял, что практически не разбираюсь в математике
- Автор:
  jaylenkelley
- 5 лет назад
- 0
$(1+x)^n=\Sigma_{k=0}^n (C_n^k*x^k)$ докажем методом математической индукции:1) проверим для любого n. Пусть n=1 $(1+x)^1=\Sigma_{k=0}^1(C_1^k*x^k)=C_1^0*x^0+C_1^1*x^1=1+x$ 2) пусть верно для nдокажем равенство для n+1Для этого распишем данную сумму подробнее: $(1+x)^n=(C_n^01+C_n^1*x^1+C_n^2*x^2+..+C_n^n*x^n)$ запишем эту сумму для n+1 $(1+x)^{n+1}=(1+x)*(1+x)^n=$ $=(1+x)*(C_n^01+C_n^1*x^1+C_n^2*x^2+..+C_n^n*x^n)=$ раскроем скобки $=(C_n^01+C_n^1*x^1+C_n^2*x^2+..+C_n^n*x^n)+ +x*((C_n^01+C_n^1*x^1+C_n^2*x^2+..+C_n^n*x^n))$ $(C_n^01+C_n^1*x^1+C_n^2*x^2+..+C_n^n*x^n)+ +((C_n^01*x+C_n^1*x^2+C_n^2*x^3+..+C_n^n*x^{n+1}))$ соберем подобные слагаемые: $C_n^01+x(C_n^1+C_n^0)+x^2(C_n^1+C_n^2)+...x^n(C_n^{n+1}+C_n^n)+x^{n+1}(C_n^n)$ теперь правило $C_n^n+C_n^{n-1}=C_{n+1}^n; C_{n}^n=C_{n+1}^{n+1}$ преобразуем нашу сумму: $C_n^01+x(C_{n+1}^1)+x^2(C_{n+1}^2)+...x^n(C_{n+1}^{n})+x^{n+1}(C_{n+1}^{n+1})=$ $= \Sigma_{k=0}^{n+1}(C_{n+1}^k*x^k)$ Что и требовалось доказатьДополнительно докажу: $C_n^p+C_n^{p+1}=C_{n+1}^{p+1}$ $\frac{n!}{p!(n-p)!}+ \frac{n!}{(p+1)!(n-p-1)!} = \frac{n!(p+1)+n!(n-p)}{(p+1)!(n-p)!}= \frac{(n+1)!}{(p+1)!(n-p)!}=C_{n+1}^{p+1}$
- Автор:
  enrique837
- 5 лет назад
- 0
Добавить свой ответ