-
выручайте, помогите решить с объяснениями по 1, а остальные, если такие же то я пойму(болела долго, теперь не пойму) №179(а,в) и №180 (желательно весь)
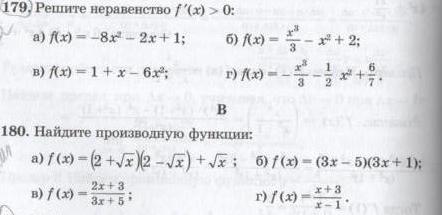
Ответы 1
-
1) f`(x)=(-8x²-2x+1)`=(-8x²)`+(-2x)`+(1)`= -8·2x-2= - 16x-2 f`(x)>0 -16х - 2 > 0 -16x>-2 x < 1/83) f`(x)=(1+x-6x²)`=(1)`+(x)`+(-6x²)`=1-12x f`(x)>0 1 -12х > 0 -12x>-1 x < 1/121) f(x)=(2+√x)(2-√x)+√x= 4-x+√x f`(x)=(4-x+√x)`= (4)`+(-x)`+(√x)`=-1+(1/(2√x))2) f(x)=(3x-5)·(3x+1)формула производной произведения: (u·v)`=u`·v+u·v` f`(x)=(3x-5)`·(3x+1) + (3x-5)·(3x+1)`=3·(3x+1)+(3x-5)·3= 3·(3x+1+3x-5)=3·(6x-4)=18x-12 3) формула производной дроби: (u/v)`=(u`·v-u·v`)/v² f`(x)=((2x+3)`·(3x+5) - (2x+3)·(3x+5)`)/(3x+5)²=(2·(3x+5)-(2x+3)·3)/(3x+5)²==(6x+10-6x-9)/(3x+5)²==1/(3x+5)²
-
Автор:
mariahnwdh - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
как записать по английски 22 января
-
Предмет:
Английский язык -
Автор:
bug - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Определить кол-во натуральных чисел, которые можно закодировать 1 байтом
-
Предмет:
Информатика -
Автор:
small - 6 лет назад
-
Ответов:
5 -
Смотреть
-
-
Переставив буквы жыонн и запиши слово
-
Предмет:
Русский язык -
Автор:
jennyaguirre - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
когда сила трения видна
-
Предмет:
Физика -
Автор:
emanueltxi5 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
