-
Вычислить. Тригонометрия.
Даю много баллов! Хэлп)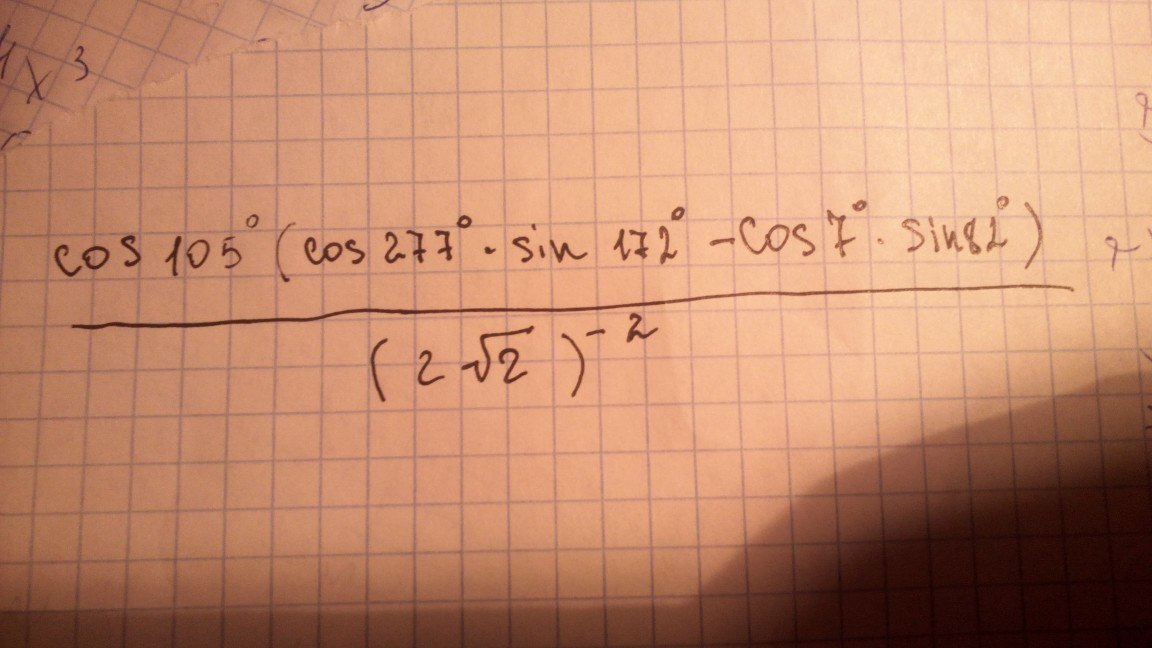
-
Предмет:
Алгебра -
Автор:
marinmercer - 5 лет назад
-
Ответы 1
-
[cos105⁰(cos277⁰sin172⁰-cos7⁰sin82⁰]/(2√2)⁻²==(2√2)²·cos105⁰·[1/2(sin(172⁰-277⁰)+sin(172⁰+277⁰))-1/2(sin(82⁰-7⁰)+sin(82⁰+7⁰))]==4·2·1/2·cos105⁰·(sin(-105⁰)+sin449⁰-sin75⁰-sin89⁰)==4·cos105⁰·(-sin105⁰+sin(2π+89⁰)-sin75⁰-sin89⁰)==-4·cos105⁰·sin105⁰-4·cos105⁰·sin75⁰==-2·sin210⁰-4·1/2·(sin(75⁰-105⁰)+sin(75⁰+105⁰)==-2sin(π+30⁰)-2[(sin(-30⁰)+sin180⁰)]==-2(-sin30⁰)-2[(-sin30⁰)+0]=2sin30⁰+2sin30⁰=4sin30⁰=4·(1/2)=2
-
Автор:
jasperyocb - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- напишите пожалуйста эти ответы правильно записаны или нет и если есть ошибка поесните её пожалуйста
- задача,,измерьте объём комнаты в вашей квартире и вычислити массу и вес воздуха в ней считая что его плотность равна 1,29 килогг. на метр в кубе ,,
-
Помогите написать сочинение на тему:Проблема взаимопонимания детей и-взрослых в произведениях Льва толстого и а Бунина
-
Предмет:
Литература -
Автор:
stitchohpr - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
Составте хронологическую таблицу "Греко- персидские войны" Дата, событие, значение
-
Предмет:
История -
Автор:
victorinowise - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
