-
Построить график функции и определить, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку
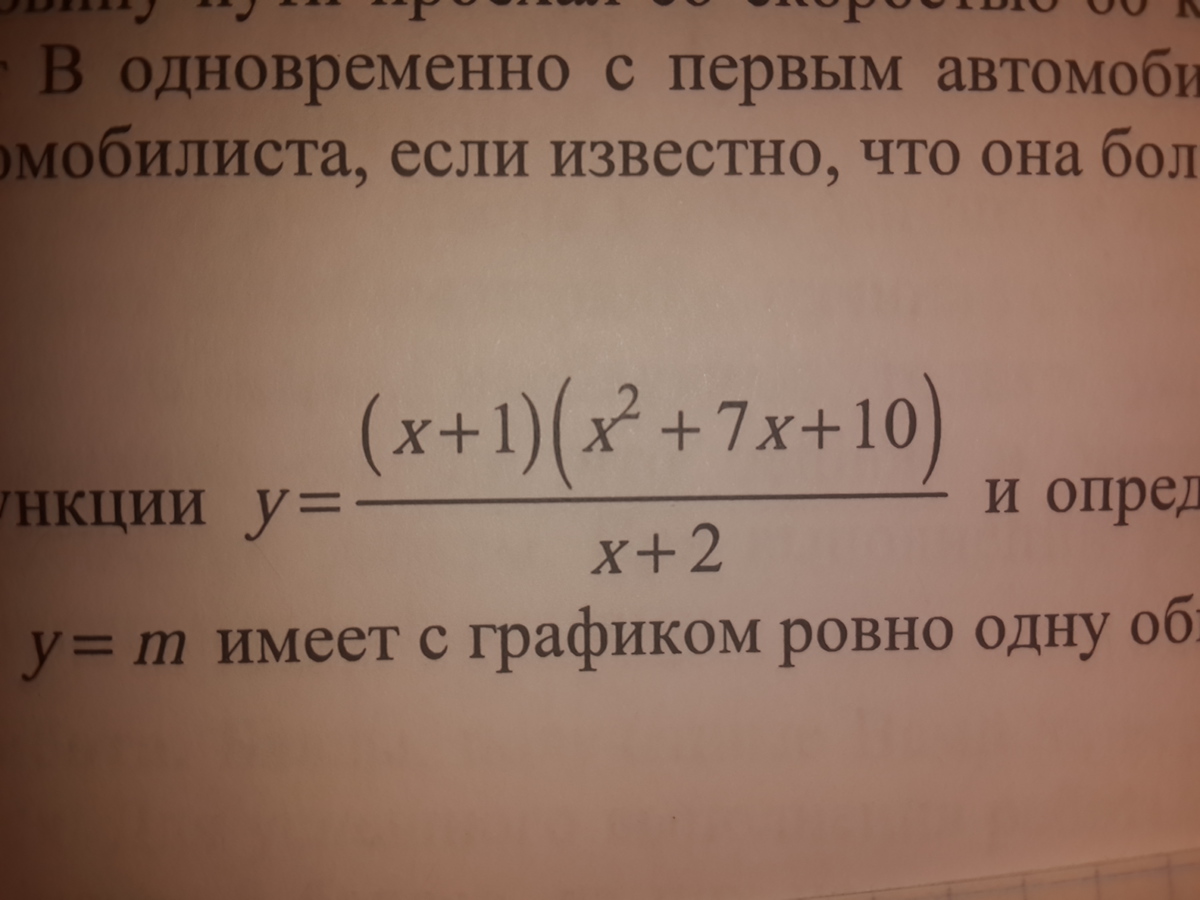
-
Предмет:
Алгебра -
Автор:
elishakane - 6 лет назад
-
Ответы 1
-
Раскладываем квадратный трехчлен в числителе на множители:x^2 + 7x + 10 = 0Находим корни по теореме, обратной теореме Виета:x1 = -2x2 = -5Тогда трехчлен раскладывается на следующие множители:x^2 + 7x + 10 = (x + 2)(x + 5)Возвращаемся к функции:Получаем дробь (x + 1)(x + 2)(x + 5)/(x + 2)Дробь сократимая на (х + 2), но т.к. (х + 2) стоит в знаменателе, то x не должен быть равен -2Итак, у нас функция: y = (x + 1)(x + 5); (x не равен -2)Раскрываем скобки, получаем:y = x^2 + 6x + 5Теперь у нас квадратичная функция, графиком которой является парабола, ветви которой направлены вверх (т.к. коэффициент перед x^2 положительный)Найдем координаты вершины параболы: абсцисса (х) = -b/a = -6/2 = -3ордината (у) = (-3)^2 + 6*(-3) + 5 = 9 -18 + 5 = -4Точка с координатами (-3;-4) - вершина параболы.Строим параболу (думаю, справитесь самостоятельно.)Теперь найдем значения m, при которых прямая y=m имеет с графиком ровно одну общую точку.Это встречается в двух местах:1) на вершине параболы следовательно m будет равно ординате (у) вершины праболы, т.е. m=-42) как мы помним, у нас было условие, что x не должен равняться -2, следовательно точка, которая должна лежать на параболе с абсциссой -2 отсутствует, значит ордината этой точки и будет вторым искомым значенимем m.Подставляем в наше уравнение -2 вместо х:y=(-2)^2 + 6*(-2) + 5 = -3.m = -3 -второе значение
-
Автор:
sageyzpj - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Какова жизнь Кашириных в повести "Детство"? Пожалуйста, дайте развёрнутый ответ.
-
Предмет:
Литература -
Автор:
janessao3fi - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Частицы с какими электрическими зарядами отталкиваются?
-
Предмет:
Физика -
Автор:
raymondrichards - 6 лет назад
-
Ответов:
2 -
Смотреть
-
- (x-3)(x+5)-(x²+x) как решить помогите плиз, заранее спасибо)
-
ПОМОГИТЕ ПОЖАЛУЙСТА!!! ХОТЯ БЫ ЧЕМ СМОЖЕТЕ((((
1. Опорные структуры: одноклеточных, плоских кольчатых и круглых червей, членистоногих, рыбы, земноводных, пресмыкающихся, птицы и млекопитающих.
How much to ban the user?
1 hour
1 day
100 years
