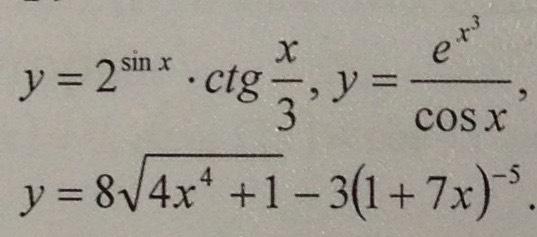Ответы 2
-
-
Автор:
dillonnedm - 6 лет назад
-
0
-
-
y' = 2^sinx*ln2*cosx*ctg(x/3)+2^sinx*(-1/[sin(x/3)]^2)*1/3==2^sinx(ln2*cosx*ctg(x/3)-1/3[sin(x/3)]^2 e^(x^3)*3x^2*cosx -e^(x^3)*(-sinx) 3x^2 tgx y'= ------------------------------------------------- = e^(x^3)* (------------ + ---------) (cosx)^2 cosx cosx
-
Автор:
myliesjra - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
напишите формулу средней линии правильного треугольника
-
Предмет:
Математика -
Автор:
jaguarualf - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Коктем туралы шыгарма керек
-
Предмет:
Другие предметы -
Автор:
lucanodouglas - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Преобразуйте в многочлен выражение (3+а)в кубе
-
кем становится головастик когда вырастит
-
Предмет:
Русский язык -
Автор:
jaliyahmckenzie - 6 лет назад
-
Ответов:
3 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years