-
Распишите ПОДРОБНО решение номера 926,пожалуйста (хотя бы пункта "а").
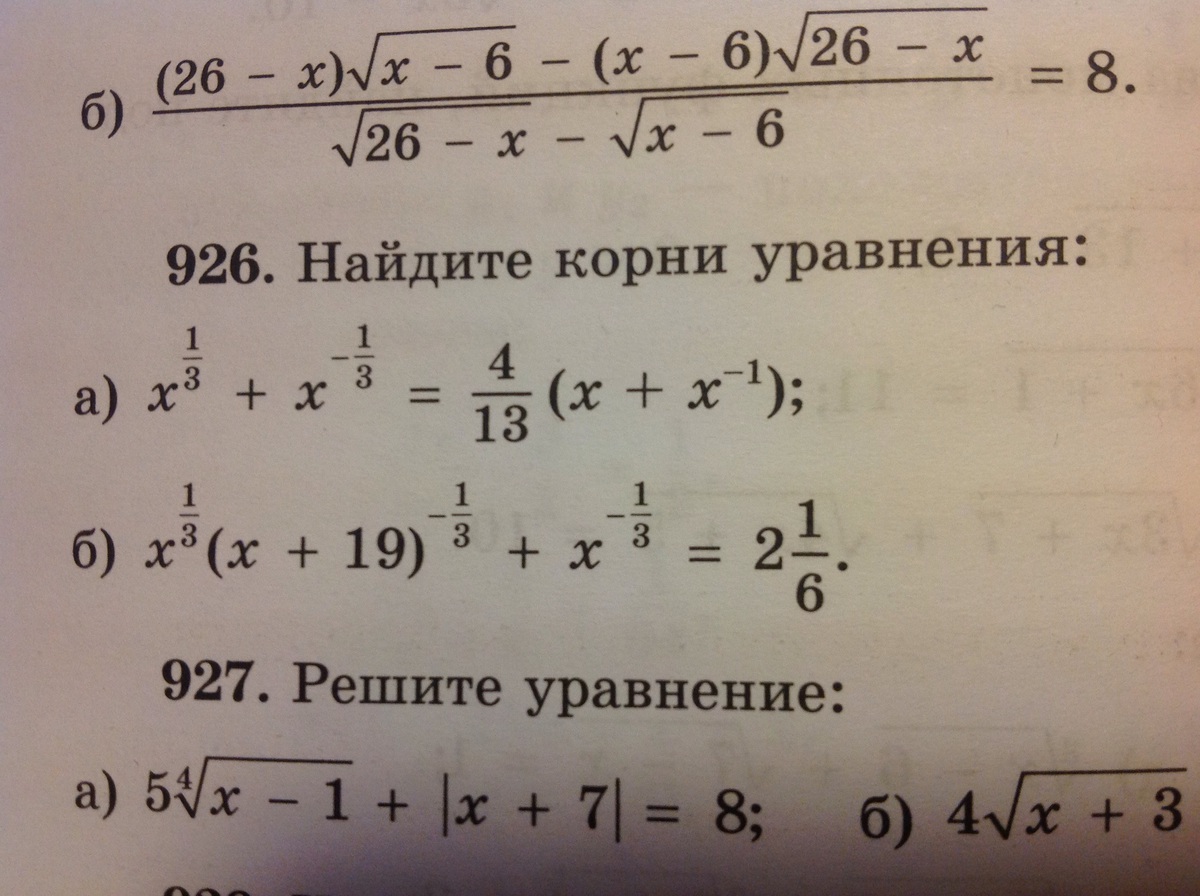
-
Предмет:
Алгебра -
Автор:
hannahren0 - 6 лет назад
-
Ответы 2
-
Огромное спасибо!!!
-
Автор:
moriahharding - 6 лет назад
-
0
-
-
Сделаем замену
Тогда по формуле суммы кубов
получим
Перепишем данное уравнение относительно уже замены
возвращаемся к замене1)
решений нет2)
3)
ответ: -8;-1/8;1/8;8
-
Автор:
hayes - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
какие стороны прямоугольника образуют прямой угол
-
Предмет:
Математика -
Автор:
cloedickson - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Длина аквариума прямоугольной формы 90 см, ширина равна 2/3 длины, а высота составляет 5/6 ширины. Найди объем аквариума
-
Предмет:
Математика -
Автор:
honeyud4s - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
найдите неизвестные слагаемые 150+х=255
-
Предмет:
Математика -
Автор:
weirdowvwy - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Какие типы экономических районов можно выделить в территориальной структуре стран???
-
Предмет:
География -
Автор:
jaggerandersen - 6 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
