Задать вопрос Регистрация
Помочь другим

  • Математики!Срочно на помощь!
    Помогите,пожалуйста, с заданием по алгебре!
    Задание находится на фото, во вложениях.
    Распишите все максимально подробно!!! Это важно!!!
    Заранее спасибо!!!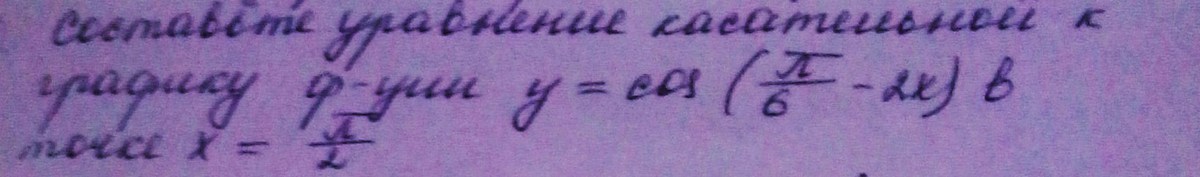

    question img

Ответы 2

  • Уравнение касательной имеет видy = kx+b, где k=y'(x0)Найдем производнуюy' = - sin(пи/6 -2x) *(-2) = 2* sin(пи/6-2x)y'(пи/2) = 2*sin(пи/6 - пи) = -2*sin (пи/6) =-2*0,5 = -1Значит, уравнение касательной имеет видy = -x+b Для нахождения b найдем значение заданной функции в т. x0 =пи/2y (x0) = cos (пи/6 - 2*пи/2) = cos(пи/6 - пи)= -cos (пи/6) = - корень(3)/2Тогда-пи/2+b =  - корень(3)/2b = пи/2 - корень(3)/2и уравнение касательной в т.  x0 = пи/2 будетy = -x + пи/2 - корень(3)/2

    • Автор:

      gracetodd
    • 6 лет назад
    • 0
  • y=cos(\frac{\pi}{6}-2x)\; ,\; x_0=\frac{\pi}{2}\\\\k=y'=2sin(\frac{\pi}{6}-2x)\\\\y'(x_0)=y'(\frac{\pi}{2})=2sin(\frac{\pi}{6}-\pi )=-2sin\frac{\pi}{6}=-1\\\\y(x_0)=y(\frac{\pi}{2})=cos(\frac{\pi}{6}-\pi )=-cos\frac{\pi}{6}=-\frac{\sqrt3}{2}\\\\y=y(x_0)+k(x-x_0)\\\\y=-\frac{\sqrt3}{2}-1\cdot (x-\frac{\pi}{2})\\\\y=-x+\frac{\pi}{2}-\frac{\sqrt3}{2}\\\\y=-x+\frac{\pi -\sqrt3}{2}

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years