-
срочно,помогите пожалуйста)никак не сходится с ответом)№909
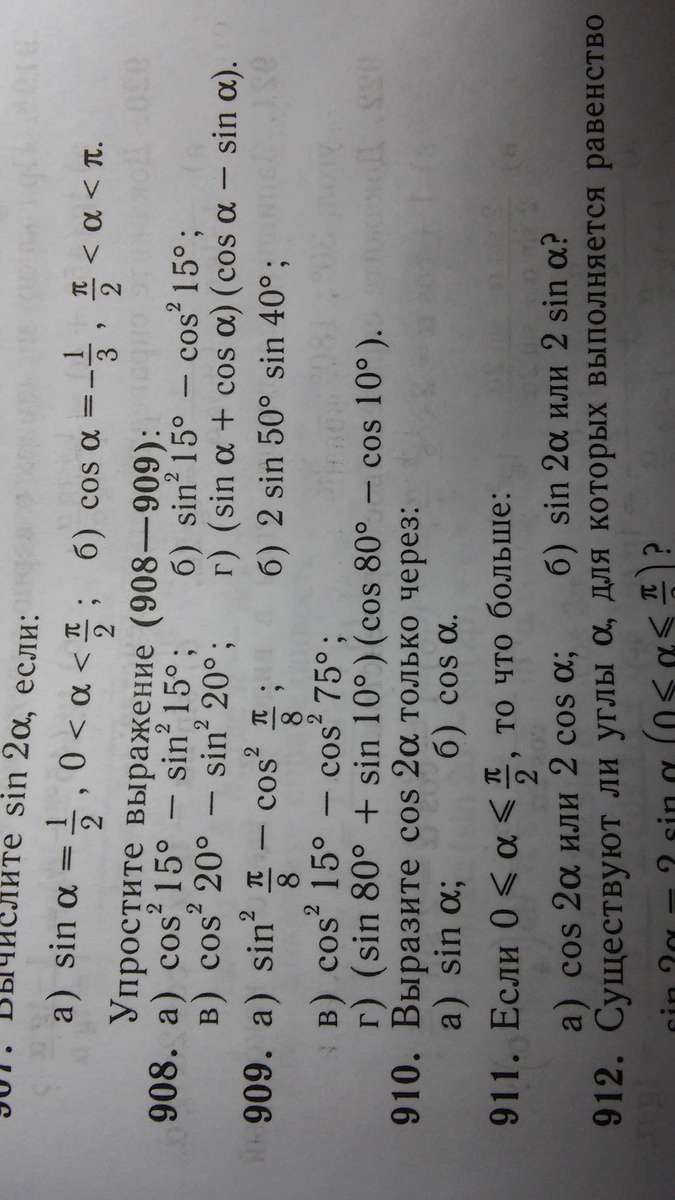
Ответы 3
-
В п. б) забыли на 2 умножить. Но эти преобразования очень долго делать. Лучше пользоваться формулами для дополнительных углов.
-
Автор:
reillygalloway - 5 лет назад
-
0
-
-
909.a) sin²(π/8)-cos²(π/8)=-(cos²(π/8)-sin²(π/8)=-cos(π/4).б) 2*sin50°*sin40°. По формуле преобразования произведения тригонометрических функций в сумму имеем:(сos(50°-40°)-cos(50°+40°)/2=(cos10°-cos90°)/2=(cos10°)/2.в) cos²15°-cos²75°=-(cos²75°-cos²15°)=-(cos75°+cos15°)(cos75°-cos15°). По формулам преобразования суммы и разности тригонометрических функций в произведение имеем:-(2*cos((75°+15°)/2)*cos((75°-15°)/2))*(-2 (sin((75°+15°)/2)*sin((75°-15°)/2))=4*cos45°*cos30°*sin45°*sin30°=4*√2/2*√3/2*√2/2*1/2=√3/2.г) (sin80°+sin10°)*(cos80°-cos10°)По формулам преобразования суммы и разности тригонометрических функций в произведение имеем:2*sin45°*cos35°*(-2)*sin45°*sin35°=-2*√2/2*cos35°*√2/2*sin35°==-2*sin35°*cos35°*1/2*=-sin70°.
-
Автор:
keaton - 5 лет назад
-
0
-
-
-
Автор:
nguyen - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
1)где солнце стоит в зените 22 декабря?
2)22 июня за Северным полярным кругом день иди ночь?
3)22 декабря за Северным полярным кругом день или ночь ?
4)какое полушарие 21 марта освещение лучше ?
5)где солнце в зените 21 марта ?
6)где 5-6 месяцев длится полярная ночь и день ? - (a^2\a+n - a^2\a^2+n^2+2an) \ (a^2\a-n - a^2\a^2-n^2)
-
С какой интонацией надо произносить слова льва и какаду
-
Предмет:
Математика -
Автор:
lawrence6 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
- Мотоциклист за первые 2 часа проехал 90 км а следующие 3 часа 50 км/ч Средняя скорость пути составляет?
How much to ban the user?
1 hour
1 day
100 years
