-
решите,пожайлуста уравнение[tex] \frac{x^{2}+ax+4-a }{x(x+1)} =0[/tex]
очень надо:3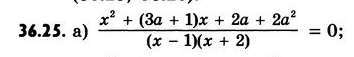
-
Предмет:
Алгебра -
Автор:
maximilianbarnett - 6 лет назад
-
Ответы 1
-
х≠0 и х≠-1x²+ax+4-a=0D=a²-4(4-a)=a²+4a-16≥0 (рисунок к решению в файле приложения)корни многочлена Д=16+4*16=80 a1=-4-4√5/2=-2-2√5 a2=-4+4√5/2=-2+2√5при а=-2-2√5 и а=-2+2√5 уравнение имеет 2 одинаковых корнях=-а/2=-(-2-2√5)/2=1+√5 при а=-2-2√5х=-а/2=-(-2+2√5)/2=1-√5 при а=-2+2√5при а∈(-∞;-2-2√5)∨(-2+2√5;∞) уравнение имеет 2 различных корня корнях=-а+√(а²+4а-16)/2х=-а-√(а²+4а-16)/2проверим при каком значении а корни равны 0 или -1х1=0-а+√(а²+4а-16)/2=0√а²+4а-16=аа²+4а-16=а²4а-16=0а=4при а=4 исходное уравнение примет видх²+4х/х(х+1)=0х(х+4)/х(х+1)=0исходное уравнение имеет 1 корень х=-4х2=0√(а²+4а-16)=-аа²+4а-16=а²4а-16=0а=4 не является корнем уравнения √(а²+4а-16)=-а, т.к. корень не может быть отрицательнымх1=-1-а+√а²+4а-16/2=-1-а+√а²+4а-16=-2√а²+4а-16=а-2а²+4а-16=а²-4а+48а=20а=2,5 не является корнем уравнения √(а²+4а-16)=а-2, т.к. корень не может быть отрицательнымх2=-1-а-√а²+4а-16/2=-1-а-√а²+4а-16=-2√а²+4а-16=-а+2а²+4а-16=а²-4а+48а=20а=2,5при а=2,5 исходное уравнение примет видх²+2,5х+1,5/х(х+1)=0(х+1)(х+1,5)/х(х+1)=0уравнение имеет один корень х=-1,5при а∈(-2-2√5;-2+2√5) корней нетОтвет: при а∈(-2-2√5;-2+2√5) корней нетпри а=4,а=2,5 а=-2-2√5, а=-2+2√5 уравнение имеет один кореньх=-4, х=-1,5; х=1+√5; х=1-√5при а∈(-∞;-2-2√5)∨(-2+2√5;2,5)∨(2,5;4)∨(4;+∞) уравнение имеет 2 корнях=-а+√(а²+4а-16)/2х=-а-√(а²+4а-16)/2
x²+(3a+1)x+2a+2a²=0D=(3a+1)²-4(2a+2a²)=9a²+6a+1-8a-8a²=a²-2a+1=(a-1)²≥0неравенство верно при любом аД=0 а=1х²+4х+4/(х-1)(х+2)=0(х+2)²/(х-1)(х+2)=0 - уравнение не имеет корней при а=1Д>0 уравнение числителя имеет 2 корняx1=-(3a+1)+|a-1|/2x2=-(3a+1)-|a-1|/2выясним при каком а корни уравнения (у числителя) равны 1х1=1-(3а+1)+|a-1|/2=1-3a-1+|a-1|=2|a-1|=3+3aa-1=3+3a или a-1=-3-3a-2a=4 4a=-2a=-2 a=-1/2a=-2 не является корнем уравнения |a-1|=3+3a, т.к. модуль не может быть отрицательнымпри а=-0,5 исходное уравнение примет видх²-0,5х-0,5/(х-1)(х+2)=0(х-1)(х+0,5)/(х-1)(х+2)=0уравнение имеет один корень х=-0,5х2=1-(3а+1)-|a-1|/2=1-3a-1-|a-1|=2|a-1|=-3-3aa-1=3+3a или a-1=-3-3a-2a=4 4a=-2a=-2 a=-1/2a=-1/2 не является корнем уравнения |a-1|=-3-3a, т.к. модуль не может быть отрицательнымпри а=-2 исходное уравнение имеет вид х²-5х+4/(х-1)(х+2)=0(х-1)(х-4)/(х-1)(х+2)=0уравнение имеет один корень х=4Ответ: при а=1 уравнение корней не имеетпри а=-2 и а=-1/2 уравнение имеет 1 корень х=4 и х=-0,5при а∈(-∞;=2)∨(-2;-0,5)∨(-0,5;1)∨(1;+∞) уравнение имеет 2 корняx1=-(3a+1)+|a-1|/2x2=-(3a+1)-|a-1|/2
-
Автор:
phoebecsrk - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
запиши качества которые по твоему мнению должны быть у скомороха
-
Предмет:
Другие предметы -
Автор:
teagansuarez - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
(БИОЛОГИЯ)почему водоросли относят к низшим растениям.где обитают одноклеточные водоросли.какое строение имеет хламидомонада.где обитают и каоке строение имеют зелёные многоклеточные водоросли .где обитают и какое строение имеют бурые водоросли .где обитают и какое строение имеют красные водоросли.что такое слоевище .что такое храмотофор .что такое ризоиды.почему их нельзя называть корнями.какое значение имеют водоросли в природе.как человек использует водоросли.
-
Предмет:
Биология -
Автор:
amparoking - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
Первая морская победа римлян?
-
Предмет:
История -
Автор:
charliepq31 - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
Ребят, помогите пожалуйста с 273, очень надо) в ответах равно 9, но я не знаю как к этому ответу прийти(
-
Предмет:
Геометрия -
Автор:
haidenschaefer - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
