-
Помогите!
1) Найдите наибольшее целое значение а, при котором система имеет два решения.
2) При каких значениях а, уравнение имеет два различных отрицательных корня.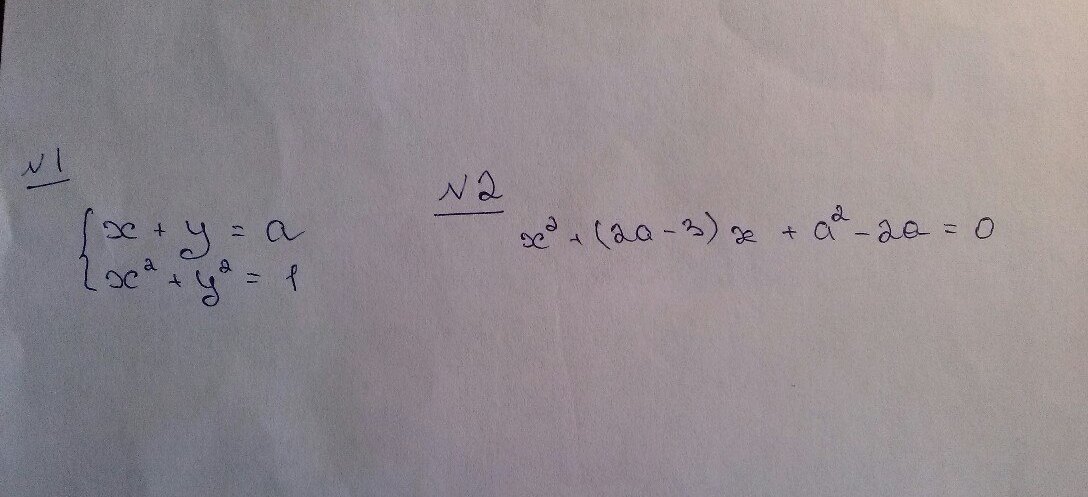
Ответы 1
-
- 1Давайте выразим x из первого уравнения и подставим его во второе.x = a - y(a-y)^2 + y^2 = 1Рассмотрим более подробно последнее уравнение. Раскроем в нём скобки и поглядим, к чему дело придёт.(y-a)^2 + y^2 = 1y^2 - 2ay + a^2 + y^2 - 1 = 02y^2 - 2ay + a^2 - 1 = 0Итак, мы получили квадратное уравнение. Для того чтобы уловить ответ на вопрос задачи, давайте рассмотрим это уравнение и x = a - y вместе. Что мы знаем о квадратном уравнении? Оно имеет либо два различных решения, либо имеет одно решение, либо же вовсе их не имеет. Сразу можем отмести последний случай - если нет корней у уравнения, то дальше и говорить не о чем.Пусть квадратное уравнение имеет единственный корень. Ну тогда смотрим, что будет с уравнением x = a-y. Оно тоже имеет одно решение, что довольно очевидно. Понятное дело, что единственному y соответствует лишь единственный x.А вот случай двух различных корней нам полностью подходит. Когда квадратное уравнение имеет два корня? Очевидно, когда его дискриминант положителен. Ищем D:D = 4a^2 - 8(a^2-1) = 4a^2 - 8a^2 + 8 = -4a^2 + 8Исходя из изложенного-4a^2 + 8 > 0a^2 - 2 < 0Решением неравенства служит интервал (-sqrt2; sqrt2). Все такие а и есть решение задачи. нам же нужно выбрать наибольшее целое из этого интервала. sqrt2 - это приблизительно 1.4, значит, наибольшее целое - это a = 1 2Присматриваемся к уравнению некоторое время, и замечаем, что оно квадратное.Подумаем, когда же квадратное уравнение может иметь два различных отрицательных корня. Ну во-первых, корней должно быть два и они должны быть различными. Эту ситуацию у нас "обслуживает" дискриминант. Совершенно понятно, что для двух различных корней он должен быть положителен. Так, с этим разобрались. А вот что дальше? Дискриминант не обеспечивает же то, каковы корни по знаку, значит нам нужно что-то ещё. И это что-то - теорема Виета. Вспомните: если у нас есть уравнение x^2 + bx + c = 0, то для него справедливо следующее: 1)x1 * x2 = c, 2)x1 + x2 = -bЗдесь x1 и x2 - корни квадратного уравнения.Как мы этим воспользуемся? А очень просто. Если оба корня отрицательны, то из произведение положительно, а сумма отрицательна. Значит, у нас x1 * x2 > 0, а x1 + x2 < 0. Останется просто записать это всё через теорему Виета. Основную идею мы нашли. Теперь приступим к реализации.x1 + x2 = 3 - 2a, а x1 * x2 = a^2 - 2aТогда для выполнения требования нам нужно, чтобыD > 03 - 2a < 0a^2 - 2a > 0Осталось найти D, решить полученную систему и получить ответ.D = (2a-3)^2 - 4(a^2 - 2a) = 4a^2 - 12a + 9 - 4a^2 + 8a = -4a + 9-4a + 9 > 04a - 9 < 0a < 9/43-2a < 02a > 3a > 3/2a^2 - 2a > 0a(a - 2) > 0Решением этого неравенства служит объединениеa < 0 и a > 2Осталось решения этих трёх неравенств пересечь между собой, и мы получаем окончательный ответ: 2< a < 9/4
-
Автор:
rapunzellu3b - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Исправьте ошибку в предложении " девушка выглядит еще глупее "
-
Предмет:
Русский язык -
Автор:
urielqqjj - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Раскройте смысл данных фразеологизмов и составьте с ними предложения. Запишите три предложения.Пользуйтесь в случае необходимости толковыми и фразеологическими словарями
Яблоко раздора
Бег на месте,
Ветер в голове,
Лакомый кусочек,
Спустя рукава,
Мастер на все руки,
Волосы дыбом встали,
Кто в лес, кто по дрова-
Предмет:
Русский язык -
Автор:
mangojoza - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Выбери правильные утверждения о составе слова. Отметь ответы .
1. В слове может не быть приставки.
2.В слове может не быть суффикса.
3.В слове может не быть окончания.
4.В слове может не быть корня.
Рядом с каждым из выбранных тобой утверждений запиши одно слово из списка, которое его подтверждает. Слова: городок, пальто, дно, кенгуру, стена, зонтик, лопата,полёт,выход,льдина-
Предмет:
Русский язык -
Автор:
moreno - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
твір ''Людина це цінність''
-
Предмет:
Українська література -
Автор:
frances - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
