-
130 баллов!!!ССЮЮЮЮДАААРешите 4 логарифмических неравенства,надо знать,как они решаются,с меня лучший ответ.
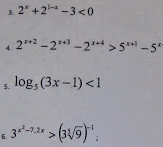
Ответы 10
-
Есть ошибка
-
Автор:
murphy - 5 лет назад
-
0
-
-
Сейчас испрвлю
-
Автор:
savanahraymond - 5 лет назад
-
0
-
-
Большое спасибо,жду
-
Автор:
parisg7eo - 5 лет назад
-
0
-
-
Изменил
-
Автор:
pennyconrad - 5 лет назад
-
0
-
-
а что, так сильно нравится математика, что далеко продвинулись? ;)
-
Автор:
martha3ja7 - 5 лет назад
-
0
-
-
слушайте, напишите в ЛС
-
Автор:
gemaknight - 5 лет назад
-
0
-
-
здесь просто немного не место. Если есть вопросы, напишите туда, я подскажу что-нибудь
-
Автор:
samantha38au - 5 лет назад
-
0
-
-
просто нас забанить могут за такие проделки ;)
-
Автор:
kayla - 5 лет назад
-
0
-
-
Если вопросы есть, как написать туда, нажимаете на мою аватарку, заходите в мой профиль, там ссылочка есть "написать сообщение"
-
Автор:
guidoy29n - 5 лет назад
-
0
-
-
3Сделаем замену 2^x = t, t > 0 - показательная функция принимает только положительные значения, что мы и будем учитывать в дальнейшем.Тогда 2^(1-x) = 2/2^x = 2/tНеравенство с учётом замены приобретает вид:t + 2/t - 3 < 0Можем умножить обе части неравенства на t > 0. При этом знак неравенства не меняем:t^2 -3t + 2 < 0Решаем квадратичное неравенство методом интервалов:(t - 2)(t-1) < 0Отсюда 1< t < 2Ну здесь всё хорошо вроде бы: условие t > 0 выполняетсяТеперь вспоминаем, кто такой t: 1 < 2^x < 2До сего момента специфики было не очень много. Сделали замену(в этом ничего нового нет). Теперь решать будем показательное неравенство. Для этого приведём все степени к удобному для нас основанию(то есть. к 2) 2^0 < 2^x < 2^1 2^x - возрастающая функция, поэтому 0 < x < 1 4При решении показательных неравенств приходится во многих случаях приводить все степени к одному основанию. В этом неравенстве у нас два "несовместимых" основания: 2 и 5. Значит. эта идея тут не сработает. Но зато я знаю, что 5^x > 0 - показательная функция принимает лишь положительные значения. Поэтому я спокойно смогу разделить обе части неравенства на 5^x. Но перед этим немного преобразую левую часть:4 * 2^x - 8 * 2^x - 16 * 2^x > 5 * 5^x - 5^xЗдесь я воспользовался свойствами степеней. Например, 2^(x+2) = 2^x * 2^2 = 4*2^x.далее:-20 * 2^x > 4 * 5^x-5 * 2^x > 5^xТеперь делим на 5^x > 0:-5 * (2/5)^x > 1Ну и сделали то, что хотели - пришли к одному основанию.(2/5)^x < -1/5И теперь мы видим одну важную вещь. Слева - показательная функция, которая принимает лишь положительные значения. Из нашего неравенства видно, что она меньше отрицательного значения, чего быть не может. Значит, решений у неравенства нет.
-
Автор:
veleriojcva - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
1)найдите сумму десяти первых членов геометрической прогрессии 6;2;2/3;...
2)найдите сумму первых тридцати членов арифметической прогрессии -1;-3;-5;...-
Предмет:
Алгебра -
Автор:
coreenvatf - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Рассчитайте удельную энергию связи ядра изотопа кислорода 16 и 8 О. Масса протона 1,0073 а.е.м., масса нейтрона 1,0087 а.е.м., масса изотопа кислорода 15,99491 а.е.м., масса электрона 0,00055 а.е.м
-
Предмет:
Физика -
Автор:
carsensih9 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
составь по план выходного дня и запиши по плану как ты проведешь день?
-
Предмет:
Русский язык -
Автор:
carolyn - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
вспомните строки прямую речь из сказки А.С Пушкина и Дополните ими слова автора)
1.Как взмолится золотая рыбка! Голосом молвит человечьим: .....
2.И сказал ей ласковой слово: ......
3.Приплыла к нему рыбка спросила: ....
4.Отвечает золотая рыбка: ....
5.Ещё пуще старуха бранится: .....
6.Ей старик с поклоном отвечает: ...
7.Старика старуха забранила: ....
8.Говорит старику старуха: ...........-
Предмет:
Русский язык -
Автор:
mckee - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
