-
Помогите срочно!!! Тригонометрия 10 класс Справа написаны промежутки
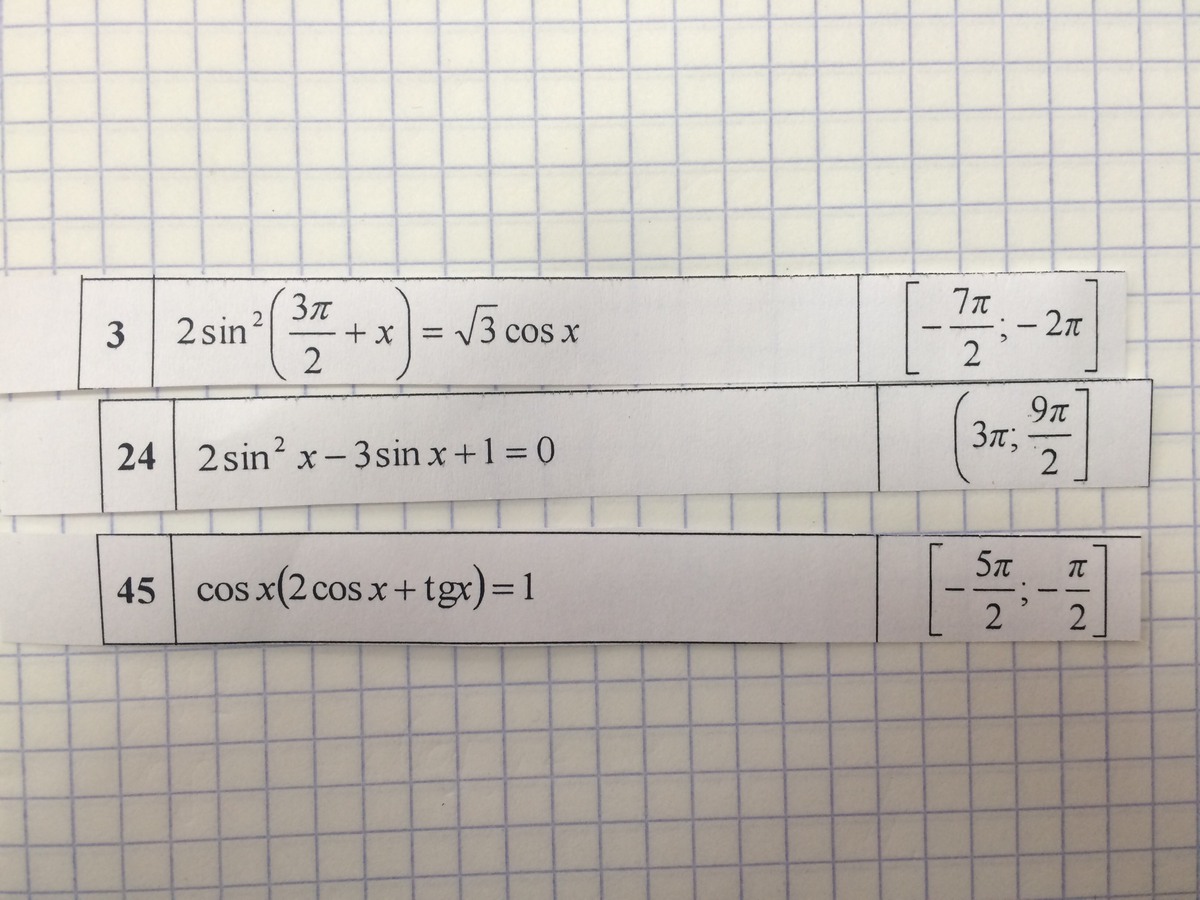
-
Предмет:
Алгебра -
Автор:
georginaxlsc - 6 лет назад
-
Ответы 1
-
3) 2sin²(3π/2+x) = √3cosx ; x∈[ -7π/2 ; -2π].2*(-cosx)² = √3cosx ;2cos²x - √3cosx = 0;2cosx(cosx - √3/2) = 0 ;[ cosx =0 ; cosx =√3/2. [ x =π/2 + π*k ; x = - π/6+2π*k ; x = π/6+2π*k ; k∈Z.Выбор корней x∈[ -7π/2 ; -2π] :- 7π/2 ≤ π/2 + π*k ≤ -2π ⇔ -7π/2 - π/2 ≤ π*k ≤ -π/2 -2π ⇔ -4π ≤ π*k ≤ -5π/2 ⇔ - 4≤k≤ -5/2 ⇒k = - 4 ; -3⇒x = -7π/2 ; x = -5π/2. из x = - π/6+2π*k ⇒x = - 13π/6 при k = - 1. из x = π/6+2π*k нет решения x∈[ -7π/2 ; -2π] .ответ : -7π/2 ; -5π/2 ; -13π/6 .============================================24) 2sin²x - 3sinx +1 =0 ; x∈ (3π ; 9π/2] .[ sinx =1/2 ; sinx =1. *** sinx = t ***[ x = ( -1)^(k)*π/6 +π*k ; x =π/2+ 2π*k , k ∈ Z .Для выбора корней удобно писать решения в виде :[ x = π/6 +2π*k ; x =(π -π/6) +2π*k ; x =π/2+ 2π*k , k ∈ Z. или тоже самое :[ x = π/6 +2π*k ; x =5π/6) +2π*k ; x =π/2+ 2π*k , k ∈ Z.ответ : π/6 +4π = 25π/4 ; x =π/2+ 4π =9π/2.===========================================45) cosx(2cosx + tqx) =1 ; x∈ [ -5π/2 ; -π/2] . 2cos²x + sinx =1 ;2(1 -sin²x) +sinx = 1;2sin²x - sinx -1 =0 ;[sinx = -1/2 ; sinx =1 ;[ x = (-1)^(k+1) π/6 +π*k ; x =π/2 +2π*k ;k ∈ Z. Для выбора корней удобно писать решения в виде :[ x = - π/6 + 2π*k ; x = -5π/6 +2π*k ; x =π/2 +2π*k ;k ∈ Z.[ x = - π/6 - 2π ; x= π/2 - 2π = - 3π/2 .ответ : - π/6 -2π = - 13π/6 ; π/2- 2π = - 3π/2.
-
Автор:
madelynnilao - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
How much to ban the user?
1 hour
1 day
100 years
