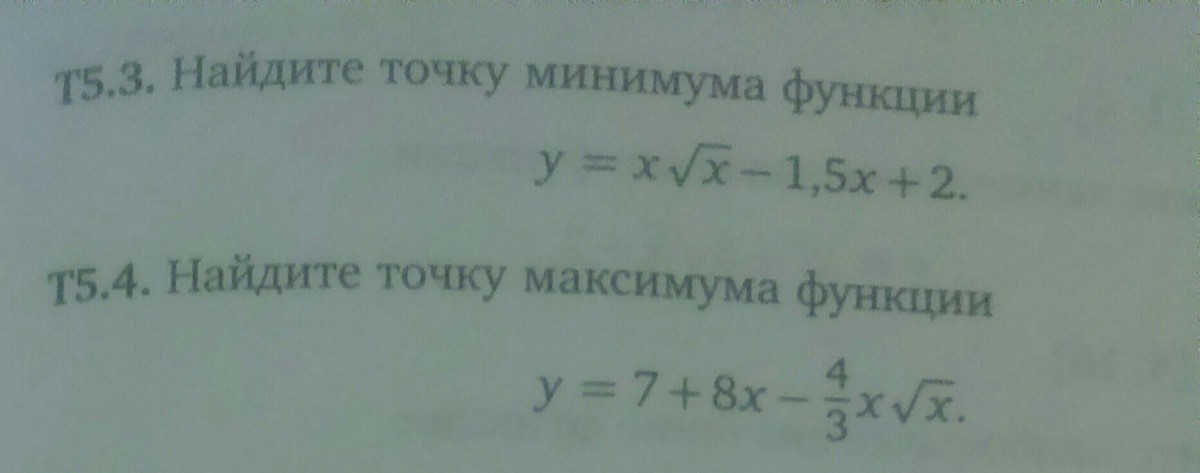Ответы 2
-
спасибо
-
Автор:
chevym5pk - 6 лет назад
-
0
-
-
1) y = x^(3/2) - 1.5*x + 2РешениеНаходим первую производную функции:y` = (3/2)*√x - 1,5илиy` = (1,5)*√x - 1,5Приравниваем ее к нулю:(1,5)*√x - 1,5 = 0√x = 1x₁ = 1Вычисляем значения функции f(1) = 1,5Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную:y`` = 3 / (4√x)Вычисляем:y''(1) = 0,75 > 0 - значит точка x = 1 точка минимума функции.2) y = 7+ 8*x - (4/3)*x^(3/2)РешениеНаходим первую производную функции:y` = - 2√x + 8Приравниваем ее к нулю:- 2√x + 8 = 0√x = 4x₁ = 16Вычисляем значения функции f(16) = 149/3Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную:y`` = - 1 / √xВычисляем:y''(16) = -1/4 < 0 - значит точка x = 16 точка максимума функции.
-
Автор:
mariodunn - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- как разделить воду и нефть
-
My future profession
-
Предмет:
Английский язык -
Автор:
lefty6qod - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
представьте число 3(целых)2/5(две пятых) в виде неправильной дроби.
-
Предмет:
Математика -
Автор:
kenya6nw0 - 6 лет назад
-
Ответов:
5 -
Смотреть
-
-
В каком предложении допущена грамматическая ошибка?
Выберите вариант ответа:
Согласно приказу директора экскурсию провели в четверг.
Дуршлаг – необходимый предмет кухонной утвари.
Старик, меля зерно, покрылся белой пылью с головы до ног.
После олимпиады я, наверно, пристрастюсь к чтению орфографического словаря.
Семиклассник, нёсший пять килограммов макулатуры, вызывал уважительные взгляды прохожих.-
Предмет:
Русский язык -
Автор:
koty - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years