Задать вопрос Регистрация
Помочь другим

  • Помогите с производной. Задание номер 1, 1 пример СРОЧНО!!! Найти производную

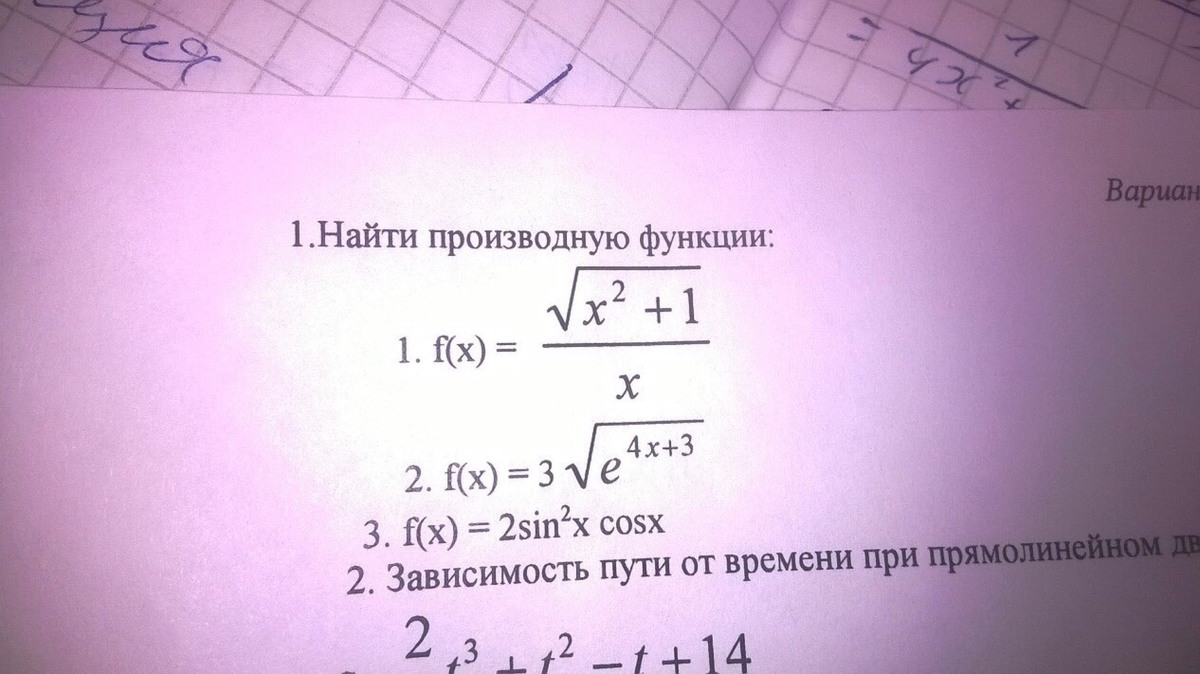
    question img

Ответы 3

  • Спасибо, Вам огромное!:))
  • не за что)))

    • Автор:

      loki66
    • 5 лет назад
    • 0
  • f(x)= \frac{ \sqrt{ x^{2} +1} }{x} f'(x)= (\frac{ \sqrt{ x^{2} +1} }{x} )'= \frac{( \sqrt{ x^{2} +1})'*x-(x)'* \sqrt{ x^{2} +1} }{ x^{2} } = \frac{ \frac{( x^{2} +1)'}{2 \sqrt{ x^{2} +1} }*x-1* \sqrt{ x^{2} +1} }{ x^{2} } =\frac{ \frac{2x}{2 \sqrt{ x^{2} +1} }*x- \sqrt{ x^{2} +1} }{ x^{2} } =\frac{ \frac{ x^{2} }{ \sqrt{ x^{2} +1} }- \sqrt{ x^{2} +1} }{ x^{2} }= \frac{ x^{2} - ( \sqrt{ x^{2} +1} )^{2} }{ x^{2} \sqrt{ x^{2} +1} }= \frac{ x^{2} - x^{2} -1}{x^{2} \sqrt{ x^{2} +1}} = \frac{-1}{x^{2} \sqrt{ x^{2} +1}}

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years