Задать вопрос Регистрация
Помочь другим

  • Решите неравенство, как можно подробнее, пожалуйста.
    Ответ такой: [-1;0) ; (0;4]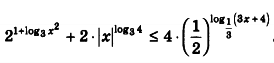

    question img

Ответы 1

  • 2^{1+ log_{3}x^2 }+ 2 | x | ^{ log_{3}4 } \leq 4* ( \frac{1}{2})^{ log_{ \frac{1}{3} } (3x+4)} ОДЗ:  x^{2} \ \textgreater \ 03x+4\ \textgreater \ 0x eq 0x\ \textgreater \ -1 \frac{1}{3} 2*2^{ log_{3}x^2 }+ 2 | x | ^{ log_{3}4 } \leq 2^2* }{2}^{ log_{ {3} } (3x+4)} 2^{ log_{3}x^2 }+ | x | ^{ log_{3}4 } \leq 2* }{2}^{ log_{ {3} } (3x+4)} 2^{ log_{3}x^2 }+ | x | ^{ log_{3}4 } \leq }{2}^{ 1+log_{ {3} } (3x+4)} 2^{ log_{3}x^2 }+ 4 ^{ log_{3} | x | } \leq }{2}^{ 1+log_{ {3} } (3x+4)} 2^{ log_{3}x^2 }+ 2 ^{ log_{3} | x |^2 } \leq }{2}^{ 1+log_{ {3} } (3x+4)} 2*2^{ log_{3}x^2 } \leq }{2}^{ 1+log_{ {3} } (3x+4)} 2^{1+ log_{3}x^2 } \leq }{2}^{ 1+log_{ {3} } (3x+4)} {1+ log_{3}x^2 } \leq }{ 1+log_{ {3} } (3x+4)} log_{3}x^2 } \leq }{log_{ {3} } (3x+4)} x^2 } \leq }3x+4} x^{2} -3x-4 \leq 0D=9+16=25x_1=4x_2=-1(x-4)(x+1) \leq 0решаем методом интервалов и получаем  x∈ [ - 1 ; 4]с учетом ОДЗОтвет: [-1;0)  (0;4]

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years