-
Вот, не могу никак прийти к решению. Вроде не так уж прям и сложно должно быть всё ведь.
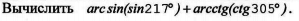
-
Предмет:
Алгебра -
Автор:
parkersimmons - 6 лет назад
-
Ответы 11
-
здесь идея другая. Обозначьте arcsin(din 217) за a
-
Автор:
haydenmbyo - 6 лет назад
-
0
-
-
дальше используем определение арксинуса.
-
Автор:
belle - 6 лет назад
-
0
-
-
не, здесь все неверно...
-
Автор:
atanasio - 6 лет назад
-
0
-
-
это формула верна только для x от -pi/2 до pi/2
-
Автор:
kirbysiit - 6 лет назад
-
0
-
-
Да, точно, давно тригонометрию не трогал. от -90 до 90
-
Автор:
gonzálezyv5o - 6 лет назад
-
0
-
-
Решение верное, ибо совпадает с ответом. Но как осуществляется этот перевод, что sin 217° = - sin 37° и такой же с катангенсом?
-
Автор:
ronanob9t - 6 лет назад
-
0
-
-
формулы приведения, мистер)))
-
Автор:
baby0bfx - 6 лет назад
-
0
-
-
Ох, точно, забыл весь школьный курс уже) Мерси!
-
Автор:
leeblackwell - 6 лет назад
-
0
-
-
на здоровье! ))
-
Автор:
roverlevy - 6 лет назад
-
0
-
-
Если мне окончательно не отшибло память, то arcsin(sin(x))=x, при -pi/2<x<pi/2. Так же и для arcctg(ctg(x))=x при 0<x<pi.
получим arcsin(-sin(37))=-37гр.
По свойству arcctg(-x)=pi-arcctg(x) получим ctg(305)=-ctg(55), тогда arcctg(-ctg(55))=180- arcctg(ctg(55))=125 гр.
Итого -37+125=88 гр.
-
Автор:
panther - 6 лет назад
-
0
-
-
sin 217° = - sin 37° => arcsin(-sin 37°) = -37°ctg 305° = - ctg 55° => arcctg(-ctg 55°) = 180° - arcctg(ctg 55°) = 180° - 55° = 125°=> -37° + 125° = 88°Ответ: 88°.
-
Автор:
obiemlkf - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
какое предложение составлено правильно?
1)a)She is agood mother.
b)She is good amother.
c)They are agood mothers.
d)They are goods mothers.
2)a) He wants to buy pair of glases.
b)They bougnt three pairs of trousers.
с)Where is my scissors?
d)I cannot find your scissors.
3)Oна никого не видела.
a)She has seen nobody.
b)She has not seen nobody
c)She did not see nobody.
d)She has seen anybody.
4) a)He is today at work at the bus station.
b)He is at the bus station at work today.
c)Today he is at work at the bus station.
d)At work he is at the bus station today.
5)a)How good of you to visit your friend!
b)What good of you to visit him!
c)What nice aman is he!
d)What she runs!
6)Джон не в доме.
a)John not in the house.
b)John is not in the house.
c)Not in the house is John.
d)John is in the house.
7)Друг моего брата.
a)My brother friend.
b)My friend brother^s.
c)My brotheк^s friend.
d)My friend brother.
8)Это комната
a)It aroom.
b)It is aroom.
c)It^s room.
d)It be aroom.
9)a)How fantastik afilm that was!
b)How fantastik afilm was that!
c)How afantastik film that was!
d) How was that film fantastik!
10)a)Whose books are these?
b)Whose are these money?
c)Whose office you have visited?
d)Whose money this is?
-
Предмет:
Английский язык -
Автор:
lili17e7 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
прямая у=5-4х касается параболы у=х2 вх с в точке с абциссой х=3. найдите сумму в с
-
Предмет:
Геометрия -
Автор:
jaggeraxof - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
вычислите, заранее спасибо (√3-√5)*(√3+√5)
-
Предмет:
Алгебра -
Автор:
maximillianyxaz - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Добути 3 простих і 7 складних речовин з Al(OH)3,HCl, P , Ba ,H2O (можно використовувати продукти взаємодіі )
-
Предмет:
Химия -
Автор:
cameronr35a - 6 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
