-
КТО-НИБУУУУДЬ. Решите неравенство подробно
ответ: (15/8 ; 2)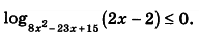
Ответы 4
-
в 10 строчке снизу должен быть знак больше)
-
Автор:
genevievebarker - 6 лет назад
-
0
-
-
Нет, меньше. У нас по условию логарифм <= 0, независимо от значения основания.
-
Автор:
smoochiercwy - 6 лет назад
-
0
-
-
хорошо, спасибо
-
Автор:
buddy0pss - 6 лет назад
-
0
-
-
У меня получилось такlog_(8x^2-23x+15) (2x-2) <= 0Во-первых, область определения{ 8x^2-23x+15 > 0{ 8x^2-23x+15 =/= 1; то есть 8x^2-23x+14 =/= 0{ 2x-2 > 0Решаем{ (x - 1)(8x - 15) > 0{ (x - 2)(8x - 7) =/= 0{ x > 1Получаем{ x = (-oo; 1) U (15/8; +oo){ x =/= 2; x =/= 7/8{ x > 1Область определения:x = (15/8; 2) U (2; +oo)Рассмотрим случайlog_(8x^2-23x+15) (2x-2) = 02x - 2 = 1x = 3/2 = 12/8 < 15/8 - не входит в область определения.Рассмотрим случай{ 8x^2-23x+15 < 1; то есть 8x^2-23x+14 < 0{ log_(8x^2-23x+15) (2x-2) < 0Решаем{ (x - 2)(8x - 7) < 0{ 2x-2 > 1Получаем{ 7/8 < x < 2{ x > 3/2{ x = (15/8; 2) U (2; +oo)Решение:x = (15/8; 2)Рассмотрим случай{ 8x^2-23x+15 > 1; то есть 8x^2-23x+14 > 0{ log_(8x^2-23x+15) (2x-2) < 0Решаем{ (x - 2)(8x - 7) > 0{ 2x-2 < 1Получаем{ x = (-oo; 7/8) U (2; +oo){ x < 3/2 = 12/8{ x = (15/8; 2) U (2; +oo)Решений нетОтвет: x = (15/8; 2)
-
Автор:
francisco478 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- помогите решить уравнение 3х=у+5 где у=2х
-
look at the picture write what was happening when the lights went out.What was each person doing?Use the verbs describe the pictures
Пример 1.Grandfather-Grandfather was reading a book when the lights want out
2.Hakim and Amir-watch televison
3.Mum-talk on the phone
4.Grandmother-eat a snack at the dinner table
5.Alisha-listen to music
6.Dad-sleep on the sofa-
Предмет:
Английский язык -
Автор:
dunnp6fk - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Помогите пожалуйста решить задачу!!! Массовая доля углерода в углеводороде равна 82, 76%. Масса 1,12 л(н.у.) этого углеводорода в газообразном состоянии равна 2,9 г. При его радикальном хлорировании может образоваться два изомерных хлоралкана, в молекулах которых атом хлора связан с первичным или третичным атомом углерода. Определите строение исходного углеводорода.
-
в семье 5 детей какова вероятность того что 2 из мальчики
-
Предмет:
Математика -
Автор:
macintosh - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
