Задать вопрос Регистрация
Помочь другим

  • Решить квадратное неравенство методом интервалов.
    Важно решение, а не ответ!Спасибо!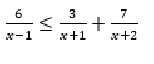

    question img

Ответы 1

  • Область определения: x =/= -2, -1, 1Переносим все налево \frac{6}{x-1} - \frac{3}{x+1} - \frac{7}{x+2} \leq 0Приводим к общему знаменателю \frac{6(x+1)(x+2) - 3(x-1)(x+2) - 7(x-1)(x+1)}{(x-1)(x+1)(x+2)} \leq 0 Раскрываем скобки \frac{6( x^{2} +3x+2)-3( x^{2} +x-2)-7( x^{2} -1)}{(x-1)(x+1)(x+2)} \leq 0Упрощаем \frac{-4 x^{2} +15x+25}{(x-1)(x+1)(x+2)} \leq 0 Умножим все неравенство на -1, при этом поменяется знак неравенства \frac{4 x^{2} -15x-25}{(x-1)(x+1)(x+2)} \geq 0Найдем корни числителяD= 15^{2} - 4*4(-25) = 225 + 400 = 625 = 25^{2} x1 = (15 - 25)/8 = -10/8 = -5/4; x2 = (15+25)/8 = 40/8=5Получаем неравенство \frac{(4x+5)(x-5)}{(x-1)(x+1)(x+2)} \geq 0 Получаем интервалы: (-oo; -2); (-2; -5/4]; [-5/4; -1); (-1; 1); (1; 5]; [5; +oo)По методу интервалов берем какое-нибудь число внутри любого интервала, например, -3, и подставляем:(-12+5)(-3-5) / [(-3-1)(-3+1)(-3+2)] = (-7)(-8) / [(-4)(-2)(-1)] < 0Значит, интервал (-oo; -2) не подходит, а подходят следующие интервалы через один: x Є (-2; -5/4] U (-1; 1) U [5; +oo)

    • Автор:

      tysongtir
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years