-
При каком положительном значении "а" система имеет единственное решение
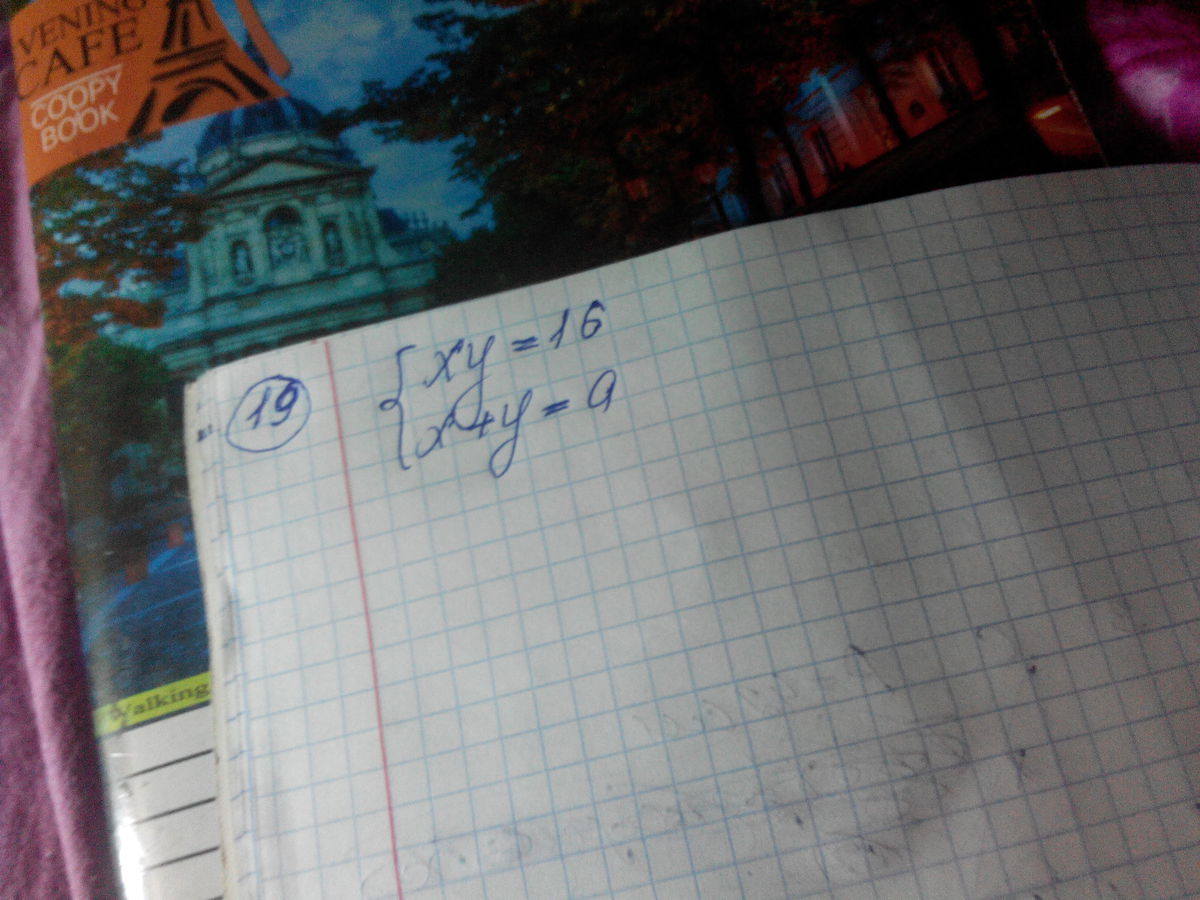
Ответы 7
-
Не совсем понимаю, зачем корни вычислять, но всё же, это больше похоже на то, что я на физмате видел=))
-
Автор:
kramer - 6 лет назад
-
0
-
-
А иначе как найти значение числа "а" и определить, что решение, т.е. корень, единственное? Может и немного запутанно, но в данный момент ничего другого не вижу. А значение "а" должно быть только положительное.=)) Я действительно училась в физмате
-
Автор:
zeus40 - 6 лет назад
-
0
-
-
Ну я ж нашёл=)) Корень один, когда Д = 0
-
Автор:
murillo - 6 лет назад
-
0
-
-
Вы-то нашли решение, а не указали окончательный ответ. Поставили + и -, а надо только +. Дали возможность что-то сделать самостоятельно и внести свой вклад в решение?=))
-
Автор:
joslynxxjf - 6 лет назад
-
0
-
-
Над фоткой ответ :D
-
Автор:
aarón23 - 6 лет назад
-
0
-
-
Ответ: 8____________

-
Автор:
scarlettwerner - 6 лет назад
-
0
-
-
Решим систему. Для этого из второго уравнения системы находим х:х = а - у. Теперь подставим в первое уравнение вместо х наше выражение:х * у=16(а - у)*у=16ау - уу -16=0 Т.е. имеем обычное квадратное уравнение. Попробуем его решить, но при этом сменим знаки на противоположные, чтобы при у^2 был знак "+".Это для того, чтобы мы не путались со знаками при дальнейшем решенииу^2 - ау + 16=0Находим дискриминант:Д= а^2 - 4*16 = а^2 - 64Находим корни уравнений а^2+ корень квадратный из (а^2 -64)у1= -------------------------------------------------------- 2 а^2 - корень квадратный из (а^2-64) у2= ----------------------------------------------------- 2Корень квадратный можно извлечь только из положительного числа. Значит наше выражение а^2 -64 должно быть больше или =0.а^2-64>=0a^2>=64 a>=8А так как нам надо, чтобы система имела лишь одно решение, т.е. один корень, то а^2 - 64 должно =0. А это возможно только при а=8.Как-то так. Не уверенна, что это правильно, но логически поразмыслив пришла именно к такому решению. Если никто ничего не предложит, можно попробовать такой способ решения.

-
Автор:
andres - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
1) Мастер до обеда забил 324 гвоздя, а после обеда он я видел еще 268 гвоздей. Сколько всего гвоздей забил мастер в течение дня?
2) Полина собрала с грядки 8 огурцов, а ее старшая сестра Надя собрала огурцов в 5 раз больше, чем Полина. Сколько огурцов собрала Надя? помогите пожалуйста умоляю-
Предмет:
Математика -
Автор:
xiomaragiles - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
Срочно нужно эссе по стихотворению К.К. Романова "12октября 1885года"
стихотворение начинается со млов:"Уж восемь лет прошло,-и снова годовщину мы Горного справляем Дубняка..."Заранее спасибо-
Предмет:
Литература -
Автор:
gloriaberry - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Человек в одежде и обуви весил 72 кг,причём одежда и обувь вместе весили на 68 кг меньше,чем сам человек.Во сколько раз меньше весили одежда и обувь,чем сам человек?
-
Предмет:
Математика -
Автор:
beamer - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Папа купил новый стол и стул. Стол стоит 56 рублей, а стул - в 8 раз дешевле стола. Какова стоимость стула?
-
Предмет:
Математика -
Автор:
precious47 - 6 лет назад
-
Ответов:
3 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
