Задать вопрос Регистрация
Помочь другим

  • Решите, пожалуйста
    Надо решить уравнение
    Картинка прилагается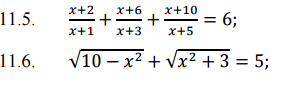

    question img

Ответы 1

  • 11.5. \frac{x+2}{x+1} + \frac{x+6}{x+3} + \frac{x+10}{x+5}=6 \frac{x+2}{x+1}= \frac{x+1+1}{x+1}= 1+\frac{1}{x+1} Аналогично \frac{x+6}{x+3}=1+ \frac{3}{x+3} ; \frac{x+10}{x+5}=1+ \frac{5}{x+5} Получаем1+ \frac{1}{x+1} +1+ \frac{3}{x+3} +1+ \frac{5}{x+5} =6 \frac{1}{x+1} + \frac{3}{x+3} + \frac{5}{x+5} =3Если x > 0, то 1/(x+1) < 1; 3/(x+3) < 1; 5/(x+5) < 1.Тогда их сумма не может равняться 3.Если -1<x<0 или -3<x<-1 или  -5<x<-3, то сумма не может быть целой.Если x < -5, то сумма вообще отрицательна.Остается единственное решение: x = 01/1 + 3/3 + 5/5 = 1 + 1 + 1 = 311.6. \sqrt{10- x^{2} } + \sqrt{ x^{2} +3}=5 Область определения x^{2} \leq 10; - \sqrt{10} \leq x \leq \sqrt{10} Возведем в квадрат все уравнение10- x^{2} +2 \sqrt{(10- x^{2})( x^{2} +3)}+ x^{2} +3=25 2 \sqrt{(10- x^{2})( x^{2} +3)}=25-10-3=12 \sqrt{- x^{4}+7 x^{2} +30} =6- x^{4}+7 x^{2} +30=36 x^{4} -7 x^{2} +6=( x^{2} -1)( x^{2} -6)=0x1=-1; x2=1; x3=- \sqrt{6} ; x4= \sqrt{6} Они все попадают в область определения.

    • Автор:

      rosebud
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years