Задать вопрос Регистрация
Помочь другим

  • Помогите решить неравенство с логарифмами! Я понял что логарифмы нужно приравнять к общему основанию, но как тут это сделать.

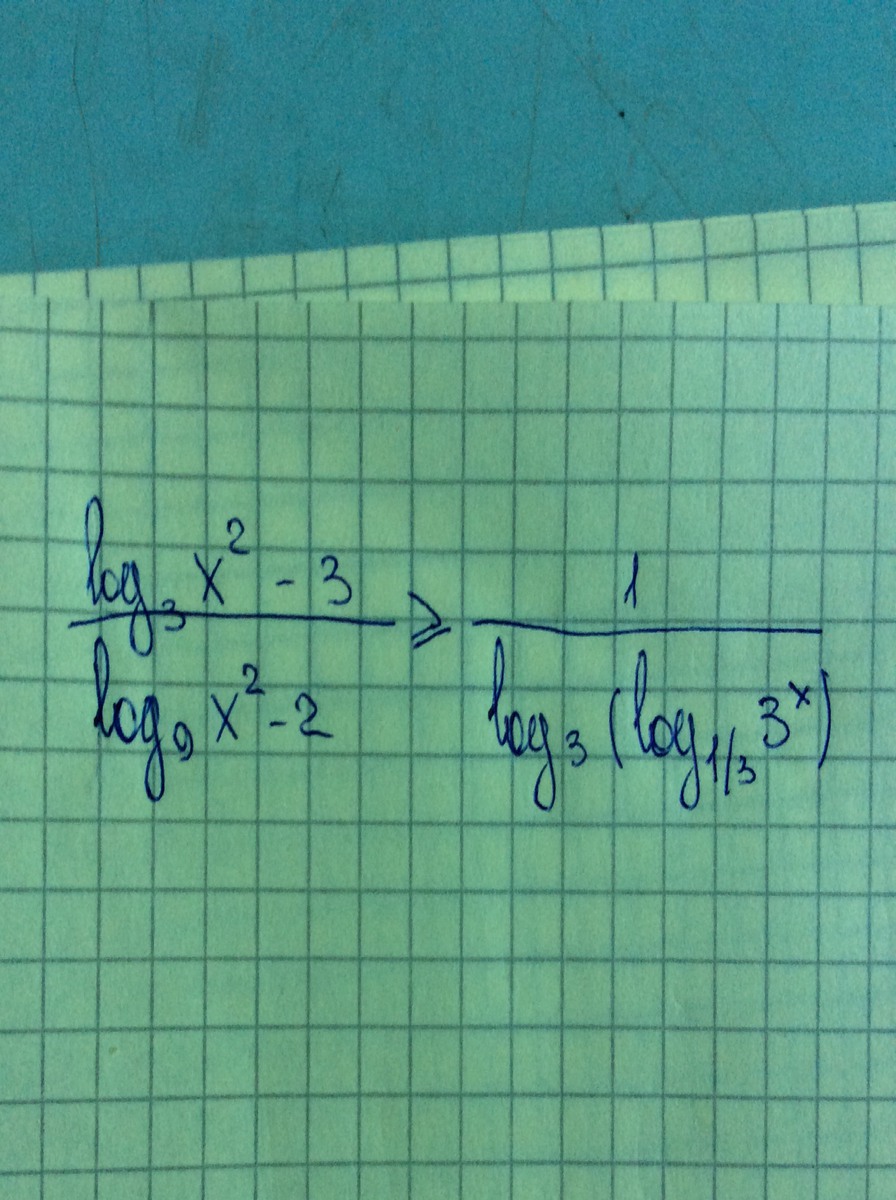
    question img

Ответы 1

  • \frac{\log_3x^2-3}{\log_9x^2-2} \geq \frac{1}{\log_3(\log_{\frac{1}{3}}3^x)}, \\ \left \{ {{x^2\ \textgreater \ 0,} \atop {\log_{\frac{1}{3}}3^x\ \textgreater \ 0,}} ight. \left \{ {{x eq 0,} \atop {x\log_{3^{-1}}3\ \textgreater \ 0,}} ight. \left \{ {{x eq 0,} \atop {-x\log_33\ \textgreater \ 0,}} ight. \left \{ {{x eq 0,} \atop {-x\ \textgreater \ 0,}} ight. \left \{ {{x eq 0,} \atop {x\ \textless \ 0,}} ight. x\ \textless \ 0; \frac{2\log_3|x|-3}{2\log_{3^2}|x|-2} \geq \frac{1}{\log_3(-x)}, \\ \frac{2\log_3(-x)-3}{\log_3(-x)-2} \geq \frac{1}{\log_3(-x)},\\ \log_3(-x)=t, \\ \frac{2t-3}{t-2} - \frac{1}{t} \geq 0,\frac{t(2t-3)-(t-2)}{t(t-2)} \geq 0, \\ 2t^2-3t-t+2 \geq 0, \\ 2t^2-4t+2 \geq 0, \\ t^2-2t+1 \geq 0, \\ (t-1)^2 \geq 0, \\ t\in R, \\ \log_3(-x)\in R, \\ -x\ \textgreater \ 0, \\ x\ \textless \ 0. \\ x\in(-\infty;0).

    • Автор:

      dalton
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years