Задать вопрос Регистрация
Помочь другим

  • Решите,пожалуйста
    Решить системы уравнений
    Картинка прилагается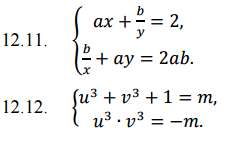

    question img

Ответы 1

  • 12.11. \left \{ {{ax+b/y=2} \atop {b/x+ay=2ab}} ight. Замена 1/y=z \left \{ {{ax+bz=2} \atop {b/x+a/z=2ab}} ight. \left \{ {{ax+bz=2} \atop { \frac{bz+ax}{xz} = \frac{2}{xz} =2ab}} ight. \left \{ {{ax+bz=2} \atop {xz=1/(ab)}} ight. Получаем теорему Виета \left \{ {{ax+bz=2} \atop {(ax)*(bz)=1}} ight. Это значит, что переменные ax и bz являются корнями уравнения t^{2} -2t+1= (t-1)^{2} =0t1=t2=1;ax=1;x=1/a;bz=b/y=1;y=bОтвет: (1/a; b)12.12. \left \{ {{ u^{3}+ v^{3}+1=m} \atop {u^{3}*v^{3}=-m}} ight. Это сразу теорема Виета \left \{ {{u^{3}+ v^{3}=m-1} \atop {u^{3}* v^{3}=-m}} ight. Это значит, что переменные u^3 и v^3 являются корнями уравнения t^{2} -(m-1)t-m=0D= (m-1)^{2} +4m= m^{2} -2m+1+4m= m^{2} +2m+1=(m+1)^{2}t1= \frac{m-1-(m+1)}{2} =-1;t2=\frac{m-1+(m+1)}{2}=m u1^{3} =-1;u1=-1; v1^{3} =m;v1= \sqrt[3]{m} u2^{3} =m;u2= \sqrt[3]{m} ; v2^{3} =-1;v2=-1Ответ: (-1: кор.куб(m)); (кор.куб(m); -1)

    • Автор:

      ivy
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years