Задать вопрос Регистрация
Помочь другим

  • Три выражения, написано упростить, но по моему тут доказать тождество

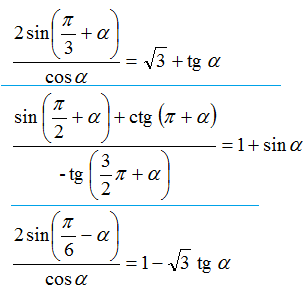
    question img

Ответы 1

  • 1.  \frac{2sin ( \frac{ \pi }{3}+ \alpha )}{cos \alpha } = \frac{2(sin \frac{ \pi }{3}*cos \alpha+sin \alpha *cos\frac{ \pi }{3})}{cos \alpha } = \frac{2(sin 60*cos \alpha+sin \alpha *cos60)}{cos \alpha } = =\frac{2(\frac{ \sqrt{3}}{2}*cos \alpha+sin \alpha * \frac{1}{2} )}{cos \alpha } = \frac{ \sqrt{3}*cos \alpha }{cos \alpha } + \frac{ sin \alpha }{cos \alpha } = \sqrt{3}+tg \alpha 2.  \frac{sin ( \frac{ \pi }{2}+ \alpha )+ctg( \pi + \alpha )}{-tg( \frac{3 \pi }{2}+ \alpha ) } = \frac{cos \alpha+ctg \alpha }{-(-ctg \alpha)}}=\frac{cos \alpha}{ctg \alpha}}+\frac{ctg \alpha }{ctg \alpha}}=sin \alpha +13. \frac{2sin ( \frac{ \pi }{6}- \alpha )}{cos \alpha }= \frac{2(sin \frac{ \pi }{6}*cos \alpha-sin \alpha *cos\frac{ \pi }{6})}{cos \alpha }= \frac{2(sin30*cos \alpha-sin \alpha *cos30)}{cos \alpha }= = \frac{2( \frac{1}{2}*cos \alpha-sin \alpha * \frac{ \sqrt{3}}{2} )}{cos \alpha }= \frac{cos \alpha }{cos \alpha } - \frac{ \sqrt{3} sin \alpha }{cos \alpha } =1- \sqrt{3} tg \alpha

    • Автор:

      lion4fxr
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years