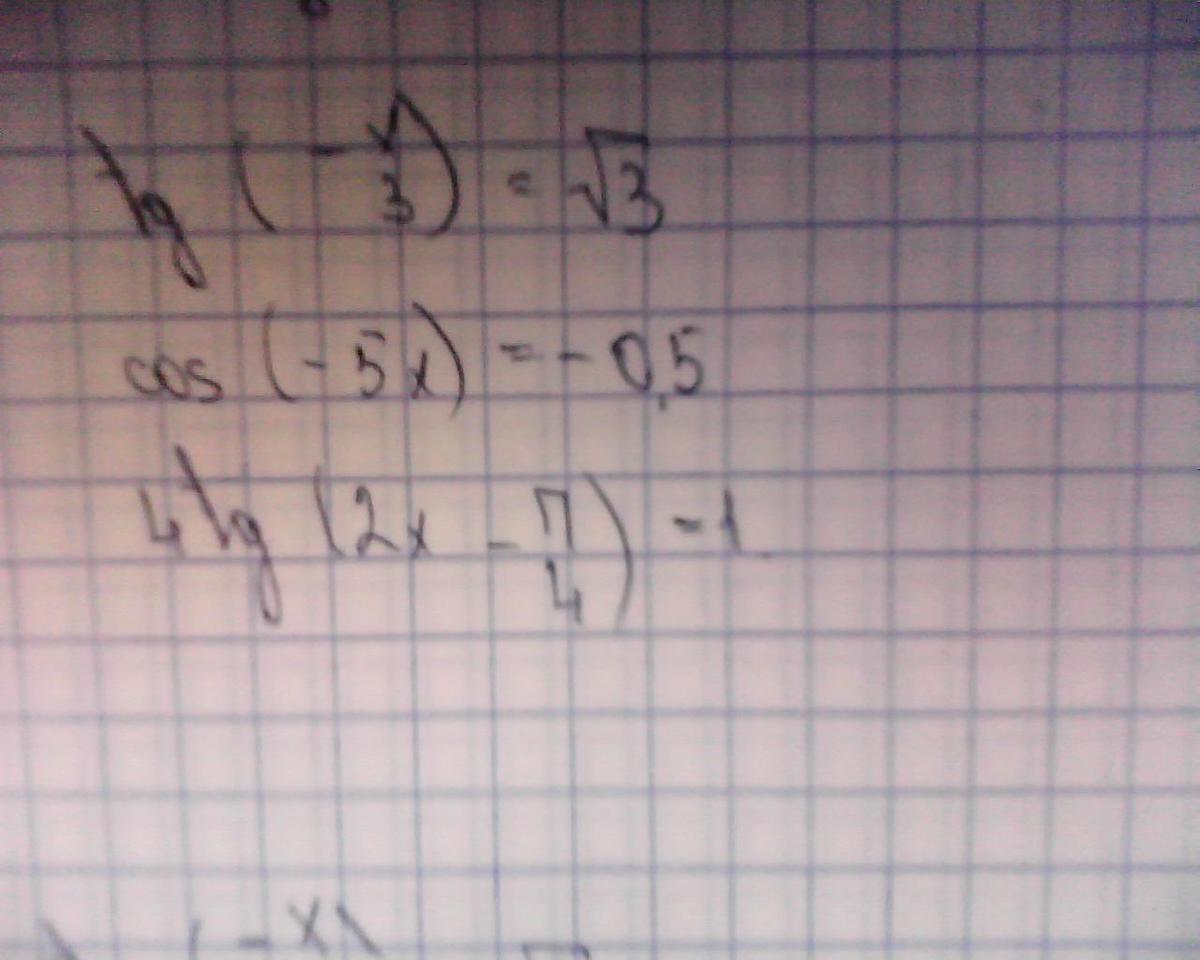Ответы 6
-
только в конце 3) x = π/8 + (1/2)*arctg(1/4) + π*k/2, k ∈Z
-
Автор:
kiersten - 6 лет назад
-
0
-
-
точно, потерял двойку. Грешен...
-
Автор:
zeus40 - 6 лет назад
-
0
-
-
спасибо
-
Автор:
valentina80 - 6 лет назад
-
0
-
-
большое спасибо за качественную и своевременную помощь)
-
Автор:
bibblessullivan - 6 лет назад
-
0
-
-
спасибо и Вам
-
Автор:
chef17 - 6 лет назад
-
0
-
-
Так как тангенс- нечетная функция, то
Так как косинус- четная функция, то
-
Автор:
english90 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Назовите наибольшую и наименьшую из величин в каждой группе А) 340мм 35см 3дм 2м 4км. Б) 2ц. 400кг 5ц. В) 4л 1дм3. 1м3. 1см 3 Помогите пожалуйста
-
Предмет:
Математика -
Автор:
hopecobb - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
3 глагола К слову УЧЕБНИК (действие в рамках темы)
-
Предмет:
Русский язык -
Автор:
eusebiobpy7 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
найди значение выражений
(21000-10986):6+894819+96318:3
1576•7+8340•4+30040-6008•5
(где деление - столбиком)-
Предмет:
Математика -
Автор:
cassiedioz - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Выразить температуры 4 К,313К, и 250 К по шкале Цельсия
-
Предмет:
Физика -
Автор:
trenton554 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years