-
Помогите с номером 8 , во вложениях! срочно ! Модераторы и анти-спамеры , не удаляйте мое задание. Там всего 1 номер , всего таких заданий 4 , я и так делю как могу.
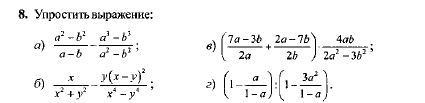
-
Предмет:
Алгебра -
Автор:
agustínhernandez - 6 лет назад
-
Ответы 2
-
a(a-b)(a+b)/(a-b) -(a-b)(a²+a+1)/(a-b)(a+b)=a+b -(a²+a+1)/(a+b)==(a²+2ab+b²-a²-ab-b²)/(a+b)=ab/(a+b)бx/(x²+y²)-y(x-y)²/(x-y)(x+y)(x²+y²)=x/(x²+y²)-y(x-y)/(x+y)(x²+y²)=(x²-xy-xy+y²)/(x+y)(x²+y²)==(x²+y²)/(x+y)(x²+y²)=1/(x+y)в(7a-3b/2a+(2a-7b)/2b=(7ab-3b²+2a²-7ab)/2ab=(2a²-3b²)/2ab(2a²-3b²)/2ab * 4ab/(2a²-3b²)=2г1- 1/(1-a)=(1-a-1)/(1-a)=-a/(1-a)1-3a²/(1-a)=(1-a-3a²)/(1-a-a/(1-a) : (1-a-3a²)/(1-a)=-a/(1-a) * (1-a)/ (1-a-3a²)=a/(3a²+a-1)
-
Автор:
robertson5 - 6 лет назад
-
0
-
-
-
Автор:
quintensi2r - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
(3.5+2 1/3):(3.5-2 1/3)=
решите полность плз-
Предмет:
Алгебра -
Автор:
fulgencioe4zs - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Ответ в квадратных сантиметрах
4 дм. в квадрате умножить на 2 минус 14 дм. в квадрате разделить на 2-
Предмет:
Математика -
Автор:
dempseybarnett - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
проверочное слова к слову веснушки проверить букву е
-
Предмет:
Русский язык -
Автор:
sethharrison - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
В ателье сшили 320 пальто за 8 дней. причём каждый день шили одинаковое количество пальто. За сколько дней сошьют 220 платьев,если ежедневно будут шить на 4 платьябольше, чем пальто?
-
Предмет:
Математика -
Автор:
brianasimpson - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
