Задать вопрос Регистрация
Помочь другим

  • найдите пожалуйста область определения функции,желательно решение добавьте во вложении

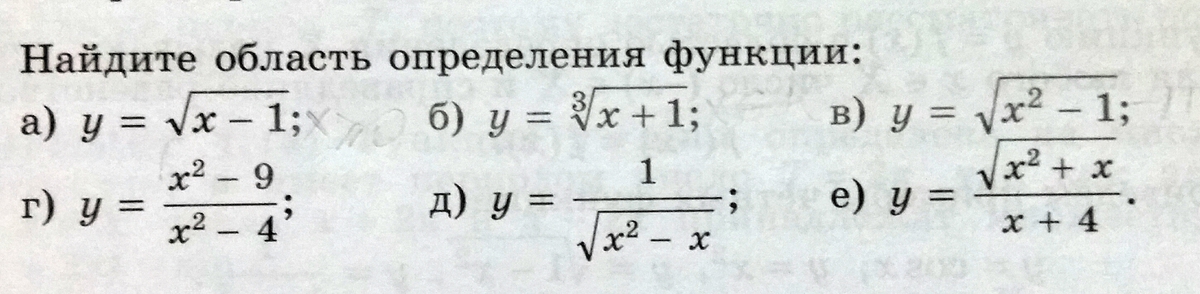
    question img

Ответы 7

  • я не понимаю ничего,что тут написано
  • страницу обнови
  • спасибо, теперь все хорошо
  • Ремарка: ответ к d читать как: действительна на всей числовой прямой кроме х=...

    • Автор:

      velasco
    • 5 лет назад
    • 0
  • спс
  • y= \sqrt{x-1} \\\ x-1 \geq 0 \\\ \boxed{x\in[1;+\infty)}y= \sqrt[3]{x+1} \\\ \boxed{x\in R}y= \sqrt{x^2-1} \\\ x^2-1 \geq 0 \\\ (x-1)(x+1) \geq 0 \\\ \boxed{x\in(-\infty;-1]\cup[1;+\infty)}y= \frac{x^2-9}{x^2-4} \\\ x^2-4 eq 0 \\\ x^2 eq 4 \\\ x eq \pm2 \\\ \boxed{x\in(-\infty;-2)\cup(-2;2)\cup(2;+\infty)}y= \frac{1}{ \sqrt{x^2-x} } \\\ x^2-x\ \textgreater \ 0 \\\ x(x-1)\ \textgreater \ 0 \\\ \boxed{x\in(-\infty;0)\cup(1;+\infty)}y= \frac{ \sqrt{x^2+x} }{x+4} \\\ \left \{ {{x^2+x \geq 0} \atop {x+4 eq 0}} ight. \\\ \left \{ {{x(x+1) \geq 0} \atop {x eq -4}} ight. \\\ \left \{ {{x\in(-\infty;-1]\cup[0;+\infty)} \atop {x eq -4}} ight. \\\ \boxed{x\in(-\infty;-4)\cup(-4;-1]\cup[0;+\infty)}
  • OD3:\\ a)x-1\geq0 \ \ \ \ \ \ \ \ \ \ \ \ \ b)x\in R\ \ \ \ \ \ \ \ c)x^2-1\geq0\\x\geq1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x^2\geq1\\.\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x\leq-1;x\geq 1\\\\d)x^2-4eq0\ \ \ \ \ \ \ \ \ \ \ \ e)x^2-x\ \textgreater \ 0\ \ \ \ f)\begin{cases}x^2+x\geq0\\xeq-4\end{cases}\\x^2eq4\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x\ \textless \ 0;x\ \textgreater \ 1\ \ \ \ \ \ x\leq -1;0\leq x\ \textless \ 4;x\ \textgreater \ 4\\xeq^+_-2\\x\in R/\{-2;2\}

    • Автор:

      selene
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years