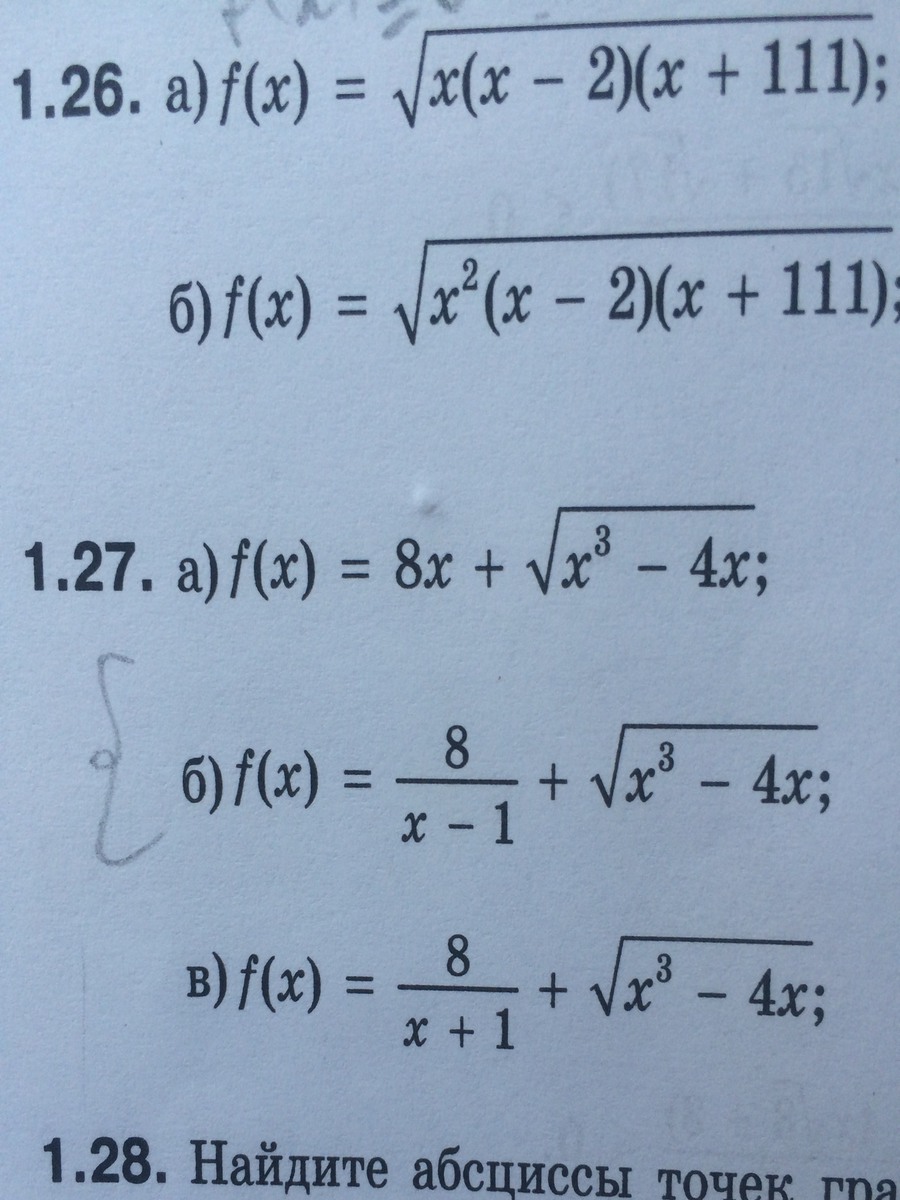1.27 а б в
решите
я чота жёстко туплю

Вообще область определения - это множество допустимых значений х. Что значит: допустимых? Допустимые значения х - это такие значения, при которых пример решается.А когда пример не решается? Нет решения:1) есть деление на нуль2) под квадратным корнем стоит отрицательное числоУ нас  есть деление только в 4 примере  и во всех примерах есть квадратный корень.Итак, начали.1)f(x) = √х(х -2)(х +111)Чтобы корень вычислялся, необходимо, чтобы выполнялось условие : х (х-2) (х +111) ≥ 0 То есть по сути надо решить неравенство. Решать будем методом интервалов:а) х = 0б) х -2 = 0    х = 2в) х + 111 = 0    х = -111Ставим эти числа на координатной прямой-∞          -111           0          2           +∞          -            -              +           +             это знаки 1 множителя (х)          -             -              -           +              это знаки 2 множителя (х-2)          -             +              +          +            это знаки 3 множителя (х + 111)Ищем, где  ≥ 0                    IIIIIIIIIIIIII             IIIIIIIIIIIIIIIIОтвет: х∈ [-111;0]∨[2; +∞)2)f(x) = √x² (x - 2)(x + 111)(x - 2)(x + 111) ≥ 0 ( x² не берём, т.к. он в квадрате, всегда ≥0)по сути надо решить неравенство. Решать будем методом интервалов:ф) х -2 = 0    х = 2б) х + 111 = 0    х = -111Ставим эти числа на координатной прямой-∞          -111                 2           +∞         -                -                  +              это знаки 1 множителя (х-2)         -               +                  +              это знаки 2 множителя (х + 111)Ищем, где  ≥ 0IIIIIIIIIIIIIIIIi                       IIIIIIIIIIIIIIIII Ответ: х ∈(-∞; -111]∨[2;+∞) 3)f(x) = 8x + √(x³ - 4x)x³ - 4x ≥ 0 x³ - 4x = 0 x(x² - 4) = 0 x = 0   или     x² - 4 = 0                        x² = 4                         x = +- 2 -∞         -2          0           2            +∞                  -            -            +          +            это знаки  х         +           -            -           +          это знаки х² - 4ищем, где ≥0                 IIIIIIIIIIII              IIIIIIIIIIIIIIIIОтвет: х∈ [-2;0]∨[2;+∞)4) f(x) = 8/(x -1) + √(x³ - 4x)Пример похож на предыдущий. Только надо добавить х-1≠0 или х≠1Самое смешное, что х = 1 не входит в ответ, так что Ответ х∈ [-2;0]∨[2;+∞)