Задать вопрос Регистрация
Помочь другим

  • Задано выражение:

    Докажите, что значение данного выражения положительно при всех допустимых значениях переменной.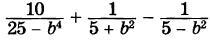

    question img

Ответы 1

  • \frac{10}{25-b^{4}}+ \frac{1}{5+b^{2}} - \frac{1}{5-b^{2}} = \frac{10}{(5+b^{2})(5-b^{2})}+ \frac{1}{5+b^{2}} - \frac{1}{5-b^{2}} = \\ =\frac{10}{(5+b^{2})(5-b^{2})}+ \frac{5-b^{2}}{(5+b^{2})(5-b^{2})} - \frac{5+b^{2}}{(5-b^{2})(5+b^{2})}= \frac{10+5-b^{2}-5-b^{2}}{(5+b^{2})(5-b^{2})} = \\ = \frac{10-2b^{2}}{(5+b^{2})(5-b^{2})} = \frac{2}{5+b^{2}}Любое число в квадрате положительно, поэтому это выражение будет принимать только положительные значения.

    • Автор:

      felicity
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years