-
здравствуйте я новичок помогите пожалуйста не возводя число в степень,сравните значения выражений.
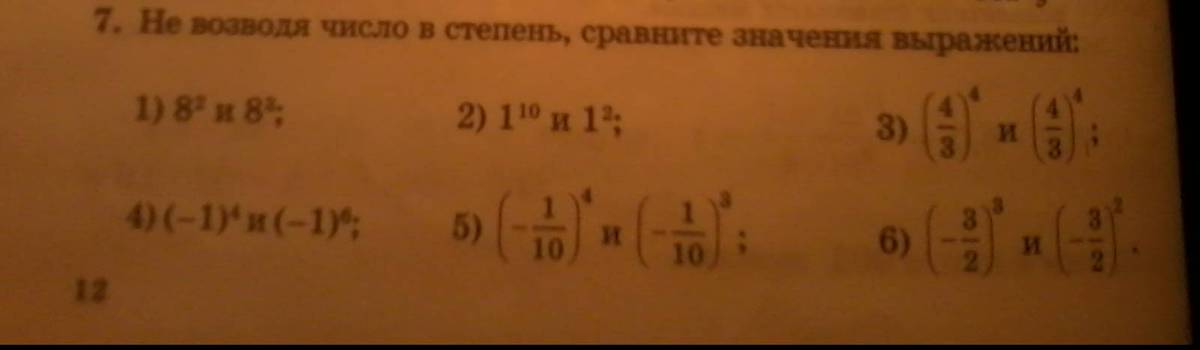
-
Предмет:
Алгебра -
Автор:
fernandoboyd - 6 лет назад
-
Ответы 4
-
спасибо большое :)
-
Автор:
rufus81 - 6 лет назад
-
0
-
-
Да на здоровье)
-
Автор:
ayla95 - 6 лет назад
-
0
-
-
Если чего-то не понятно, напиши - объясню)
-
Автор:
joy100 - 6 лет назад
-
0
-
-
В каждом примере используется один алгоритм решения, ничего другого здесь применять не надо: если основание (число, которое стоит ниже и написано "крупным шрифтом") одинаковое, что тут встречается в каждом примере, то сравнивают показатель (число, которое написано мелким шрифтом и стоит "выше"):
, так как здесь две записи абсолютно одинаковые.
, поскольку показатель первого числа (10) больше показателя второго числа (2).
, записи, опять же, одинаковые.
, здесь вновь ответ равно. Равно потому, что единица в любой степени (что в четвёртой, что в шестой (без учёта отрицательных)) будет единицей. В данном случае, число, которое нужно возвести в степень - отрицательное, поэтому применяется особое правило: для отрицательного основания важен показатель (если показатель чётный, то число станет положительным, если показатель нечётный, то число останется отрицательным). Тут число отрицательное, показатель чётный в обоих случаях (и четыре и шесть - чётные числа), поэтому ни единица в первом случае, ни единица во втором не станут отрицательными).
, здесь можно воспользоваться определённым свойством (если в определённую степень возводится дробь, то в эту степень можно возвести и числитель и знаменатель этой дроби). Однако, это свойство мы применим в последнем примере, а здесь достаточно воспользоваться правилом выше: т.к. обе дроби отрицательные, но одна возводится в чётную а другая в нечётную степени (4 и 3 соответственно), то, как мы уже знаем, число в чётной степени станет положительным, а число в нечётной останется отрицательным. Итого получаем, что первая дробь будет положительной, а вторая - отрицательной, а положительное число всегда больше отрицательного.
, механизм такой же, что и в предыдущем примере: мы не смотрим на то, насколько больше показатель первого числа показателя второго, когда мы сравниваем два числа, мы смотрим на чётности показателей этих чисел. В данном случае, первый показатель больше второго, но это нам не нужно, ибо оба числа отрицательные, а чётный показатель только у второго числа. Следовательно, вторая дробь больше.
-
Автор:
valerysheppard - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Сколько двузначных чисел можно получить,если каждый раз одно разрядное слогаемое выбирать из чисел 20, 60, 80, а другое - из чисел 5, 6, 8 ?
-
Предмет:
Математика -
Автор:
gracelynwu - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
ПОЖАЛУЙСТА, напишите значение фразеологизма ОСТАТЬСЯ С НОСОМ!!!
-
Предмет:
Русский язык -
Автор:
jaggervfle - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Каков ум,такова и речь.Хорошую речь хорошо слушать.Хороша верёвка длинная,а речь короткая. Где много слов,там мало дела.Выберите и запишите две пословицы.
-
Предмет:
Русский язык -
Автор:
zackcid6 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Несколько родовых общин,живших в одной местности. (даю 99 баллов)
-
Предмет:
История -
Автор:
teresachang - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
