-
Помогите решить! Задание по теме "производная". Все на фото
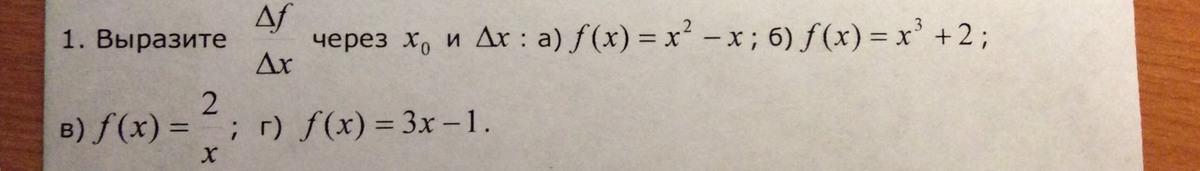
Ответы 1
-
а) f(x) =x² -x ⇒ f(xо) =xo² -xo ;1. f(xо+Δx) =(xo+Δx)² -(xo +Δx) ;2. f(xо+Δx) - f(xо) =((xo+Δx)² -(xo +Δx) ) -(xo² -xo) ;3. ( f(xо+Δx) - f(xо))/Δx =(((xo+Δx)² -(xo +Δx) ) -(xo² -xo) ) /Δx = (xo² +2xo*Δx +(Δx)² - xo - Δx -xo² +xo)/Δx =(2xo -1) + Δx ;Еще один шаг и производная этой функции готово:4) y '(xo)=Lim( f(xо+Δx) - f(xо) )/Δx =Lim( (2xo -1) + Δx )= 2xo -1. Δx→0 Δx→0-----------------------б) ( f(xо+Δx) - f(xо))/Δx = (( xo +Δx)³ +2) -(xo³ +2))/Δx =(xo³ +3xo²Δx +3xo(Δx)² +(Δx)³ +2 - xo³ -2)/Δx =3xo² + 0 +3xo(Δx) +(Δx)² .-----------------------в) ( f(xо+Δx) - f(xо))/Δx =(2/(xo+Δx) - 2/xo)/Δx =2(xo -xo - Δx)/(xo+ Δx)*xo* Δx= - 2/(xo² +xo*Δx) .-----------------------г) ( f(xо+Δx) - f(xо))/Δx =( (3(xo+Δx) -1) - (3xo -1) )/Δx =(3xo +3Δx -1 - 3xo +1)/ Δx= 3. - 0 .
-
Автор:
félix5s4f - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
На стороне AD параллелограмма ABCD отмечена точка F так,что BF=AB и угол ABF=50 градусов.Вычеслите градусные меры углов параллелограмма ABCD
-
Предмет:
Геометрия -
Автор:
bronsonferrell - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
чому в словах плаття, взуття, вугілля,гілля,знання,колосся є подвоєння букв
-
Предмет:
Українська мова -
Автор:
jesslamb - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
придумать небольшой рассказ про котенка и клубок
-
Предмет:
Русский язык -
Автор:
kallie - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
My name's Larry and I'm 9. перевод
-
Предмет:
Английский язык -
Автор:
dahlia - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
