Задать вопрос Регистрация
Помочь другим

  • Алгебра 11кл.
    Как делать такие задания? Объясните на примере одного, так как они все аналогичны по идее.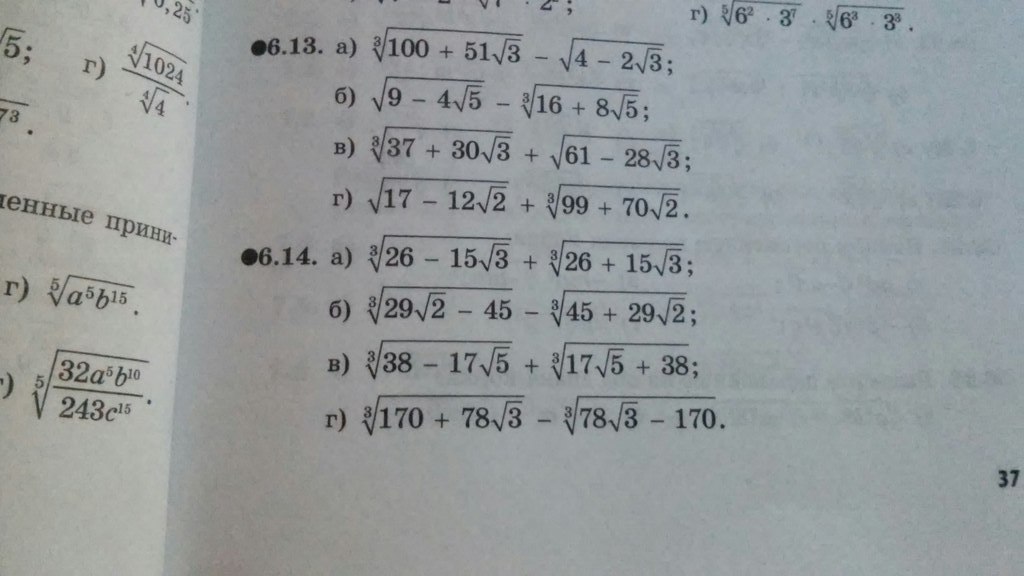

    question img

Ответы 1

  • Для решения задач такого типа нужно из выражений под знаком радикала выразить квадрат/куб суммы/разности:№ 6.13 (б)\sqrt{9-4 \sqrt{5}}- \sqrt[3]{16+8\sqrt{5}}==\sqrt{2^{2}-2*2* \sqrt{5}+(\sqrt{5})^{2}}- \sqrt[3]{(\sqrt{5})^{3}+3*(\sqrt{5})^{2}*1+3*\sqrt{5}*1^{2}+1^{3}}==\sqrt{(2- \sqrt{5})^{2}}- \sqrt[3]{(\sqrt{5}+1)^{3}}=|2-\sqrt{5}|-(\sqrt{5}+1)=-2+\sqrt{5}-\sqrt{5}-1=-3№ 6.14 (а) \sqrt[3]{26-15 \sqrt{3}}+\sqrt[3]{26+15 \sqrt{3}}=2-\sqrt{3}+\sqrt{3}+2=4, т.к: \sqrt[3]{-((\sqrt{3})^{3}-3*(\sqrt{3})^{2}*2+3*\sqrt{3}*2^{2}-2^{3})}=\sqrt[3]{-(\sqrt{3}-2)^{3}}=-(\sqrt{3}-2)=2-\sqrt{3}\sqrt[3]{26+15 \sqrt{3}}=\sqrt[3]{-((\sqrt{3})^{3}+3*(\sqrt{3})^{2}*2+3*\sqrt{3}*2^{2}+2^{3})}=\sqrt[3]{(\sqrt{3}+2)^{3}}=\sqrt{3}+2

    • Автор:

      mombod
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years