К графику функции f(x)=-8x-x^2 проведены две касательные в точках X1=-6 и x2=1. Найдите площадь треугольника, образованного этими касательными и осью ординат. ( ответ должен получиться 43,75)

Найдём уравнение касательных к графику функции f(x) = -8x-x².

f'(x) = -(8x)'-(x²)' = -8-2x

Уравнение для касательной с абсциссой точки касания x₁ = -6:

f'(x₁) =  f'(-6) = -8-2·(-6) = -8+12 = 4;

f(x₁) = f(-6) = -8·(-6)-(-6)² = 48-36 = 12;

y = f'(x₁)·(x-x₁)+f(x₁) = 4·(x-(-6))+12 = 4x+24+12 = 4x+36.

Уравнение для касательной с абсциссой точки касания x₂ = 1:

f'(x₂) = f'(1) = -8-2·1 = -8-2 = -10;

f(x₂) = f(1) = -8·1-1² = -8-1 = -9;

y = f'(x₂)·(x-x₂)+f(x₂) = -10·(x-1)+(-9) = -10x+10-9 = -10x+1.

Стороны треугольника лежат на прямых:

y = 4x+36;  y = -10x+1;  x = 0.

Найдём вершины треугольника.

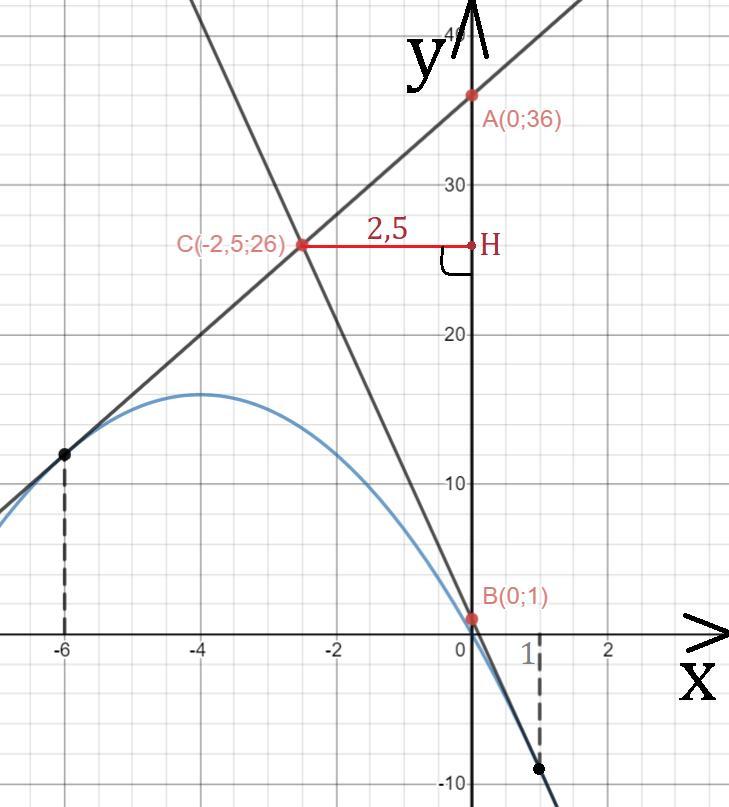
\displaystyle \left \{ {{y=4x+36} \atop {x=0\qquad \quad }} \right. \; \left \{ {{y=4\cdot 0+36} \atop {x=0\qquad \quad }} \right. ;\; A(0;36)

\displaystyle \left \{ {{y=-10x+1} \atop {x=0\qquad \quad }} \right. \; \left \{ {{y=-10\cdot 0+1} \atop {x=0\qquad \qquad }} \right. ;\; B(0;1)

\displaystyle \left \{ {{y=4x+36\quad } \atop {y=-10x+1}} \right. \; \left \{ {{4x+36=-10x+1} \atop {y=4x+36\qquad \qquad }} \right. \\\\\left \{ {{x=\dfrac{1-36}{4+10}} \atop {y=4x+36}} \right. \; \left \{ {{x=\dfrac{-5}2} \atop {y=-10+36}} \right. \\\\C(-2,\!5;26)

Сторона AB лежит на оси Oy, поэтому высота CH, треугольника ABC, будет параллельна оси Ox. А значит, CH = |-2,5| = 2,5.

AB = 36-1 = 35, поскольку эта сторона перпендикулярна оси Ох.

Площадь треугольника равна полупроизведению его высоты и стороны к которой она проведена.

S(ABC) = \dfrac12 \cdot CH\cdot AB = 2,5·35/2 = 175/4 = 43,75

Ответ: 43,75.