-
Здравствуйте. Помогите с доказательством тригонометрического выражения!
У меня при решении получается -cos^2t.
cos^2(pi-t)=-cos^2t;
sin^2(pi/2-t)=cos^2t;
cos(pi+t)=-cost;
cos(2pi-t)=cost;
tg^2(t-pi/2)=-ctg^2t;
ctg^2(3pi/2+t)=-tg^2t;
В конечном итоге имею в знаменателе 1, а в числителе -cos^2t.
В чём моя ошибка?
Прошу прощения что не использую редактор кодов, но он при выборе элементов перезагружает страницу!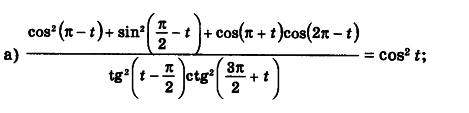
Ответы 6
-
Спасибо. Уже который раз именно после отправки вопроса нахожу решение! Моя ошибка в неправильном приведении функции tg^2(t-pi/2)! Она равна положительной функции tg^2t!
-
Автор:
wendymaxwell - 6 лет назад
-
0
-
-
*ctg^2t. Опечатка!)
-
Автор:
humbertogiles - 6 лет назад
-
0
-
-
Почему ctg^2(3pi/2+t)=tg^2t;? Ведь при наличии выражения в виде 3pi/2 в частности происходит изменение наименования тригонометрической функции, а знак ставится такой, если бы в преобразуемой функции 0<t<pi/2. Ctg^2 в таком случае будет находится в третьей четверти, где знак ctg отрицателен!
-
Автор:
evan977 - 6 лет назад
-
0
-
-
*в четвёртой четверти.
-
Автор:
salty94 - 6 лет назад
-
0
-
-
Ошибку понял. Я не обратил внимание на то, что ф-ция записана в квадрате...
-
Автор:
damarisnxrr - 6 лет назад
-
0
-
-
cos^2(pi-t)=-cos^2t; sin^2(pi/2-t)=cos^2t; cos(pi+t)=-cost; cos(2pi-t)=cost; tg^2(t-pi/2)=ctg^2t; ctg^2(3pi/2+t)=tg^2t;(cos²t+cos²t+(-cost)*cost)/ctg²t*tg²t=(2cos²t-cos²t)/1=cos²t
-
Автор:
troymorrison - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
запишите два
числа равно удаленных от числа -2 на координатной прямой"-
Предмет:
Математика -
Автор:
natashaberger - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
составить 3 предложения используя неологизмы
-
Предмет:
Русский язык -
Автор:
freedomgross - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Ученик на вопрос " сколько тебе лет?" Ответил, что через 10 лет ему будет в 5 раз больше лет , чем было 10 лет назад .сколько ему лет?
Решите уравнением-
Предмет:
Математика -
Автор:
nibblesmeadows - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
СТАВЛЮ 30 БАЛЛОВ. Хотелось бы вам побывать на необычном празднике? - Разбор предложения - составить схему., и написать чем выражен и как подчёркивается каждый член предложения...
-
Предмет:
Русский язык -
Автор:
humberto53 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
