Задать вопрос Регистрация
Помочь другим

  • Помогите с алгеброй, пожалуйста
    Докажите, что значение выражения является целым числом: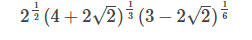

    question img

Ответы 1

  • 2^{1/2}(4+2 \sqrt{2})^{1/3}*(3-2 \sqrt{2})^{1/6}=\\\\= \sqrt{2}* \sqrt[3]{4+ \sqrt{8}}* \sqrt[6]{3- \sqrt{8} }=\\\\= \sqrt{2}* \sqrt[3]{4+ \sqrt{8} }* \sqrt[3]{ \sqrt{3- \sqrt{8} } }= = \sqrt{2}* \sqrt[3]{4+ \sqrt{8} }* \sqrt[3]{ \sqrt{ \frac{3+ \sqrt{3^2-8} }{2} }- \sqrt{ \frac{3- \sqrt{3^2-8} }{2} } }=\\\\= \sqrt{2}* \sqrt[3]{4+ \sqrt{8} }* \sqrt[3]{ \sqrt{ \frac{3+1}{2} - \sqrt{ \frac{3-1}{2} } } }=\\\\= \sqrt{2}* \sqrt[3]{4+ \sqrt{8} }* \sqrt[3]{ \sqrt{2}-1 }=\\\\= \sqrt{2}* \sqrt[3]{(4+ \sqrt{8})( \sqrt{2}-1) }=\\\\= \sqrt{2}* \sqrt[3]{4 \sqrt{2}+ \sqrt{16}-4- \sqrt{8} }=\\\\= \sqrt{2}* \sqrt[3]{4 \sqrt{2}+4-4-2 \sqrt{2} } }= =\sqrt{2}* \sqrt[3]{2 \sqrt{2} }=2^{1/2}*2^{1/3}*2^{1/6}=2^{1/2+1/3+1/6}=2^{6/6}=2^1=2\\\\2\in Z

    • Автор:

      lucy62
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years