Задать вопрос Регистрация
Помочь другим

  • Помогите, пожалуйста, упростить выражение с корнями

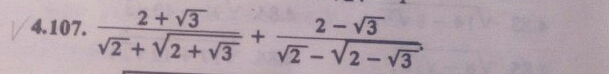
    question img

Ответы 1

  • Избавляемся от иррациональности в знаменателях: \frac{2+ \sqrt{3} }{ \sqrt{2}+ \sqrt{2+ \sqrt{3} } }+ \frac{2- \sqrt{3} }{ \sqrt{2}- \sqrt{2- \sqrt{3} } }= \\ \\ = \frac{(2+ \sqrt{3})\cdot ( \sqrt{2}- \sqrt{2+ \sqrt{3} } ) }{ (\sqrt{2}+ \sqrt{2+ \sqrt{3} })( \sqrt{2}- \sqrt{2+ \sqrt{3} } ) }+ \frac{(2- \sqrt{3})( \sqrt{2}+ \sqrt{2- \sqrt{3} } }{( \sqrt{2}- \sqrt{2- \sqrt{3} )( \sqrt{2}+ \sqrt{2- \sqrt{3} } }) }= \\ \\ = \frac{(2+ \sqrt{3})\cdot ( \sqrt{2}- \sqrt{2+ \sqrt{3} } ) }{ (\sqrt{2})^2-( \sqrt{2+ \sqrt{3} })^2 }+ \frac{(2- \sqrt{3})( \sqrt{2}+ \sqrt{2- \sqrt{3} } }{( \sqrt{2})^2-( \sqrt{2- \sqrt{3} })^2 }= \\ \\ = \frac{(2+ \sqrt{3})\cdot ( \sqrt{2}- \sqrt{2+ \sqrt{3} } ) }{ 2-(2+ \sqrt{3})}+\frac{(2- \sqrt{3})( \sqrt{2}+ \sqrt{2- \sqrt{3} } }{2-( 2- \sqrt{3} ) }==\frac{(2+ \sqrt{3})\cdot ( \sqrt{2}- \sqrt{2+ \sqrt{3} } ) }{- \sqrt{3}}+\frac{(2- \sqrt{3})( \sqrt{2}+ \sqrt{2- \sqrt{3} } )}{ \sqrt{3} }= \\ \\ =\frac{(2+ \sqrt{3})\cdot ( \sqrt{2}- \sqrt{2+ \sqrt{3} } )\cdot (- \sqrt{3}) }{3}+\frac{(2- \sqrt{3})( \sqrt{2}+ \sqrt{2- \sqrt{3} })\cdot \sqrt{3} }{ 3 }== \frac{1}{3}\cdot (-2 \sqrt{6}-3 \sqrt{2} +2 \sqrt{3}\cdot \sqrt{2+ \sqrt{3} } +3 \sqrt{2+ \sqrt{3} }+2 \sqrt{6}-3 \sqrt{2}+ \\ \\ +2 \sqrt{3}\cdot \sqrt{2- \sqrt{3} }-3 \sqrt{2- \sqrt{3} })= = \frac{1}{3}\cdot (-6\sqrt{2} +2 \sqrt{2\sqrt{3}+3 } +3 \sqrt{2+ \sqrt{3} } +2\cdot \sqrt{2\sqrt{3}-3 }-3 \sqrt{2- \sqrt{3} })

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years