-
СРОЧНО нужна помощь!ПОЖАЛУЙСТА ПОМОГИТЕ С АЛГЕБРОЙ!
РЕШИТЬ НЕРАВЕНСТВО:
a)log↓4x≤-3
б)log√3(2x-2)<2
в)log одна третья1\3 (5x-5)≥log1\3 4x
Г)log1\3(6x-3)≥log1\3 4x
Д)log0,1(2x^2-33x+13,8)<0
Е)log4x>-1\2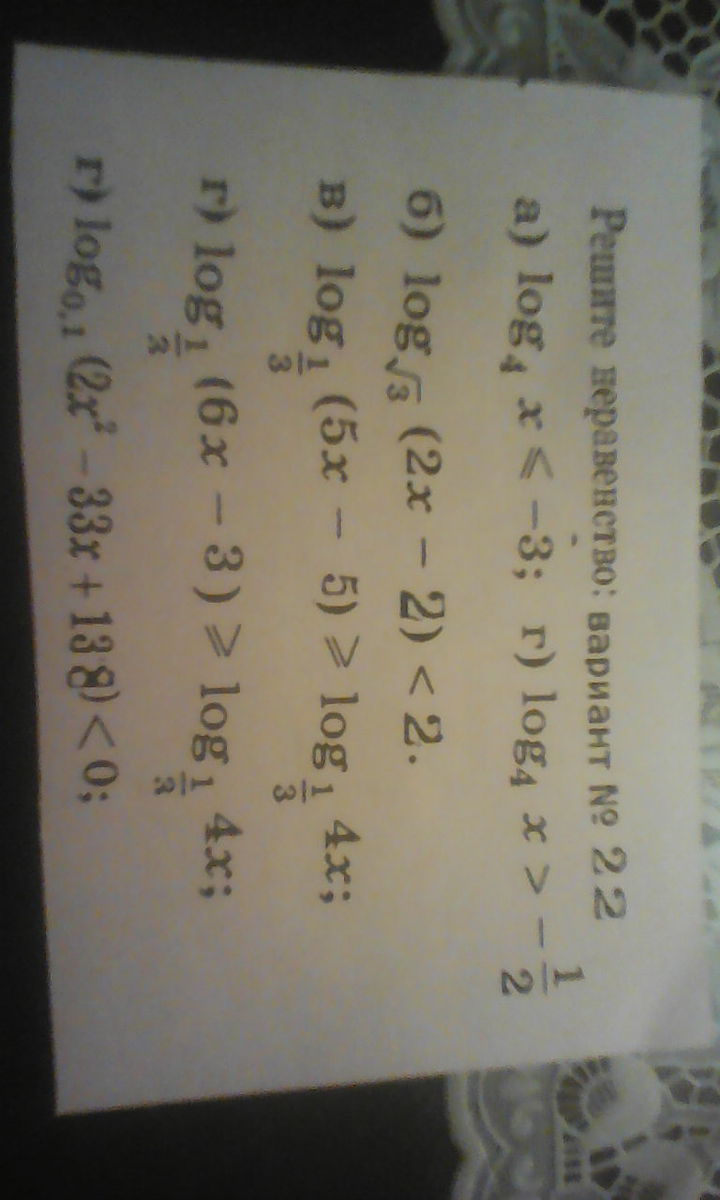
-
Предмет:
Алгебра -
Автор:
mallorygarrett - 6 лет назад
-
Ответы 6
-
Господи,большуущее тебе СПАСИБО
-
Автор:
t-dawgpiqr - 6 лет назад
-
0
-
-
пожалуйста)))
-
Автор:
oscarthornton - 6 лет назад
-
0
-
-
А это точные ответы?
-
Автор:
flintramsey - 6 лет назад
-
0
-
-
да , точные , только проверь условие д) , не нравится оно мне
-
Автор:
lucía99 - 6 лет назад
-
0
-
-
Я в вопросе отправляла картинку посмотри
-
Автор:
danikapope - 6 лет назад
-
0
-
-
а) log4 x ≤-3log4 x ≤-3log4 4 ОДЗ: x>0x≤ 4^(-3) так как основание больше единицы ( 4>1) , то знак неравенства не меняется. x≤ 1\64Ответ: х∈(0; 1\64)б)) log√3 (2x-2) <2 ОДЗ: 2х-2>0 x>1log√3 (2x-2)<log√3 (√3)²2x-2<32x<5x<2.5Ответ:х∈(1; 2.5)в) log1\3 (5x-5)≥log1\3 (4x) ОДЗ: 5х-5>0 x>1 и x>0основание логарифма меньше единицы ( 1\3<1) , значит знак неравенства меняется:5x-5≤4xx≤5Ответ:х∈(1;5]г) log1\3 (6x-3)≥log1\3 (4x) ОДЗ: х>0 и 6x-3>0 x>1\26x-3≤4x2x≤3x≤1.5Ответ: х∈(1\2 ; 1.5] д) log0.1 (2x²-33x+13.8)<0 проверьте условие , цифры плохие для решенияlog0.1(2x²-33x+13.8)<log0.1 1 ОДЗ: 2х²-33х+13,8>0 x1≈16 x2≈0.45 ++++++ 0,45--------16++++++ x∈(-∞; 0.45 ) ( 16 ; ∞)2x²-33x+13.8>12x²-33x+12.8>0 D =33²-4·2·12.8=1089-102.4=986.6 √D=√986.6≈31.4x1≈16,1 x2≈0.4 +++++++ 0,4--------16++++++ х∈(-∞;0,4)(16,1;∞)Ответ:х∈(0,4; 0,45)(16; 16.1)е) log4 x>-1\2 x>0log4 x >log4 4^(-1\2)x>1\2Ответ: х∈(1\2;∞)
-
Автор:
cecilia - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
изложение на тему самое красивое и самое уродливое
Мальчику задали в школе написать сочинение «Что ты знаешь о
самом красивом и самом уродливом». Долго думал Мальчик и не мог
сообразить, что в мире самое красивое и что — самое уродливое. Ему
казалось, что самое красивое — цветок сирени. А самой уродливой
казалась лягушка. Подошел к Дедушке, спросил: так ли это? Дедуш-
ка ответил: нет, не так.
— Самое красивое, — сказал Дедушка, — это человеческий
труд. А уродливое то, что пускает труд человеческий на ветер. Иди,
походи несколько дней по земле, и ты увидишь и то, и другое.
Пошел Мальчик. Идет полем. Видит, пшеничное поле желтеет, ни-
ва — колосок к колоску.
— Вот это и есть самое красивое, — думает Мальчик. — Ведь это
человеческий труд.
Идет дальше. Подходит к школе. Бегают дети, резвятся. Одна де-
вочка ест хлеб с маслом. Не доела, бросила кусок хлеба на землю, по-
бежала к подружкам.
— Это самое уродливое, — решил Мальчик. — Ведь она пускает
на ветер человеческий труд.
Пожалуйста помогите-
Предмет:
Русский язык -
Автор:
kahlua - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
Две силы F1=30 Н, F2=40 Н приложены к одной точке тела. Угол между векторами 90 градусов. Чему равен модуль равнодействующих этих сил?
-
Предмет:
Физика -
Автор:
damarionmeadows - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
По наклонному желобу скатываются стальной и деревянный шарики одинакового объёма.
Одинаковую ли работу совершит сила тяжести при скатывании каждого из этих шаров?
A. При скатывании деревянного шара совершается большая работа.
Б. При скатывании стального шара совершается большая работа
В. Одинаковую. -
к фразеологизмы не вешай нос подобрать синомичное слово?
-
Предмет:
Русский язык -
Автор:
cutievaldez - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
