-
Решите уравнение : помогите пожалуйста номер 1359-1360
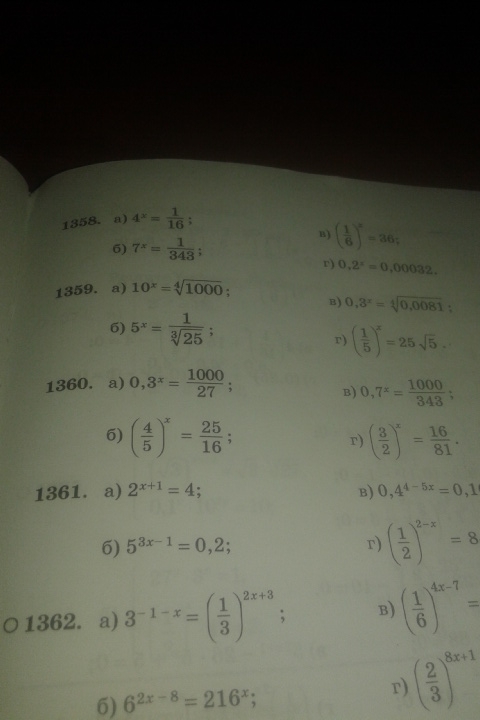
-
Предмет:
Алгебра -
Автор:
ingridserrano - 6 лет назад
-
Ответы 1
-
1359а
1359б
1359в
1359г
1360а
1360б
1360в
1360г
-
Автор:
holder - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- Работа детей в России 19 век
-
Реши уравнение x + 20 = 34 +16 ; 80 - y=12 + 8
-
Предмет:
Математика -
Автор:
spanky - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
(X-5) в квадрате +4х=25 как это решить помогите пж
-
Предмет:
Алгебра -
Автор:
adalbertogarcia - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
В трапеции АВСД АД=10 см ,а BC=6 cм.Найти среднюю линию треугольника помогите ,пожалуйста
How much to ban the user?
1 hour
1 day
100 years
