Задать вопрос Регистрация
Помочь другим

  • решите систему линейных уровнений методом гаусса и крамера , хотя бы одним каким-нибудь.очень срочно

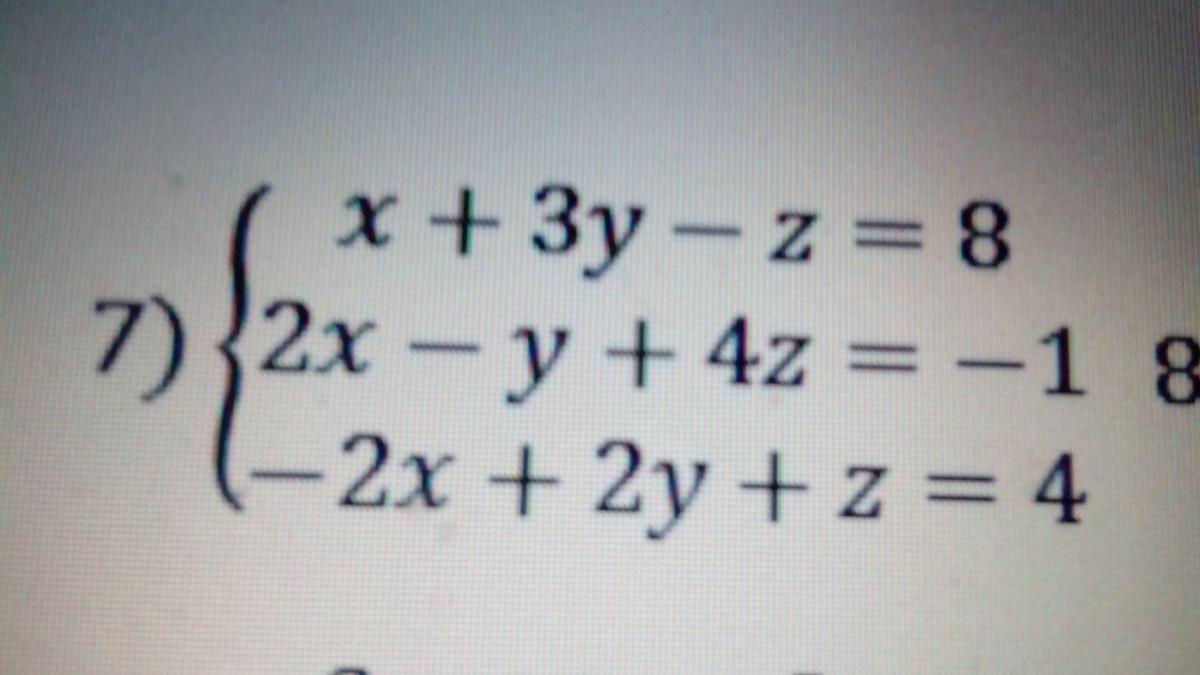
    question img

Ответы 6

  • Да, должен такой же

    • Автор:

      amaro
    • 5 лет назад
    • 0
  • хорошо, еще раз спасибо
  • А вам нужно двумя способами?
  • поидее нужно двумя но я думаю двумя никто не захочет решать вот и хотя бы один попросила

    • Автор:

      beef
    • 5 лет назад
    • 0
  • Задайте дополнительно вопрос! Метод Крамера действительно проще, если матрица не равна нулю! Гауссом можно попробовать)
  • \left\{\begin{matrix} x & + & 3y & - &z & = & 8\\ 2x& - & y & + & 4z & = & -1\\ -2x& + & 2y & + & z &= &4 \end{matrix}ight.\\Решаем матрицу методом Крамера:Находим определитель:\Delta= \begin{vmatrix}1 & 3 & -1\\2 & -1 & 4\\-2 & 2 & 1\end{vmatrix}=1\cdot(-1)\cdot1+3\cdot4\cdot(-2)+(-1)\cdot2\cdot2-(-1)\cdot(-1)\cdot(-2)-1\cdot4\cdot2-3\cdot2\cdot1=-1-24-4+2-8-6=-41\Delta_1= \begin{vmatrix}8 & 3 & -1\\-1 & -1 & 4\\4 & 2 & 1\end{vmatrix}=8\cdot(-1)\cdot1+3\cdot4\cdot4+(-1)\cdot(-1)\cdot2-(-1)\cdot(-1)\cdot4-8\cdot4\cdot2-3\cdot(-1)\cdot1=-8+48+2-4-64+3=-23\Delta_2= \begin{vmatrix}1 & 8 & -1\\2 & -1 & 4\\-2 & 4 & 1\end{vmatrix}=1\cdot(-1)\cdot1+8\cdot4\cdot(-2)+(-1)\cdot2\cdot4-(-1)\cdot(-1)\cdot(-2)-1\cdot4\cdot4-8\cdot2\cdot1=-1-64-8+2-16-16=-103\Delta_3= \begin{vmatrix}1 & 3 & 8\\2 & -1 &-1\\-2 & 2 & 4\end{vmatrix}=1\cdot(-1)\cdot4+3\cdot(-1)\cdot(-2)+8\cdot2\cdot2-8\cdot(-1)\cdot(-2)-1\cdot(-1)\cdot2-3\cdot2\cdot4=-4+6+32-16+2-24=-4x= \frac{\Delta_1}{\Delta} = \frac{-23}{-41} = \frac{23}{41}\\\\ y=\frac{\Delta_2}{\Delta}= \frac{-103}{-41}= \frac{103}{41} \\\\ z=\frac{\Delta_3}{\Delta} = \frac{-4}{-41}= \frac{4}{41}

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years