-
Помогите решить пожалуйста. Решение на листочек и подробно!!!
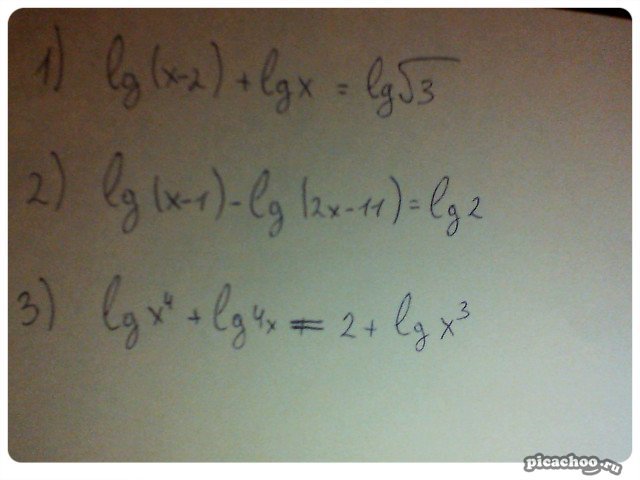
-
Предмет:
Алгебра -
Автор:
ashtonxmyv - 6 лет назад
-
Ответы 5
-
В третьем же получается один ответ, если ОДЗ x>0
-
Автор:
shylavilla - 6 лет назад
-
0
-
-
Даю
-
Автор:
belindasexton - 6 лет назад
-
0
-
-
Да.
-
Автор:
baxter - 6 лет назад
-
0
-
-
Замечательно решила, как и всегда. Я сейчас ещё скину, порешай пожалуйста.
-
Автор:
benjimyers - 6 лет назад
-
0
-
-
-
Автор:
snuffles - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
(корень5-корень45) в квадрате-(корень13+корень11)(корень11-корень13)
помогите подробно вычислить - Какие есть пустыни Африки
-
к разности чисел 842 и а прибавь 575 при а=267 ;0
-
Предмет:
Математика -
Автор:
daciano - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
литература 2 класс составить рассказ про цыпленка утку и гусей
-
Предмет:
Литература -
Автор:
salvatore - 6 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
