Показательные уравнения 1. Решите уравнение, приводя к одному основанию 2. Решите систему показательных уравнений Примеры во вложении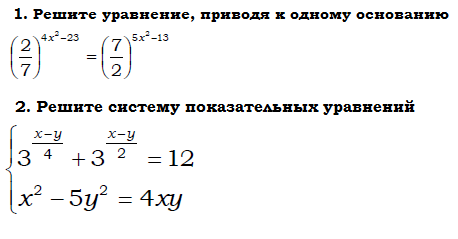

Ответы 3

Спасибо большое!
- Автор:
  lindsayblair
- 5 лет назад
- 0
Да не за что
- Автор:
  buckdfmn
- 5 лет назад
- 0
1. $( \frac{7}{2} )^{-4x^2+23}=( \frac{7}{2} )^{5x^2-13}; -4x^2+23=5x^2-13; 9x^2=36; \\ x^2=4; x=б2;$ ; Ответ: $x=б2$ 2. Для начала преобразуем первое уравнение системы. Пусть $3^{ \frac{x-y}{4} }=t; t\ \textgreater \ 0; 3^{ \frac{x-y}{2} }=t^2; t^2+t=12; t^2+t-12=0; \left \{ {{t_1+t_2=-1} \atop {t_1t_2=-12}} ight.; \\ \left \{ {{t_1=-4} \atop {t_2=3}} ight.; t\ \textgreater \ 0; t=3; 3^{ \frac{x-y}{4} }=3; \frac{x-y}{4}=1; x-y=4; y=x-4;$ Теперь полученное выражение подставим во второе уравнение системы $x^2-5(x-4)^2=4x(x-4); x^2-5(x^2-8x+16)=4x^2-16x; \\ -4x^2+40x-80=4x^2-16x; 8x^2-56x+80=0; x^2-7x+10=0; \\ \left \{ {{x_1+x_2=7} \atop {x_1x_2=10}} ight.; \left \{ {{x_1=2} \atop {x_2=5}} ight.$ . У нас получилось два значения x, каждому из них находим соответствующее значение y $\left \{ {{x=2} \atop {y=2-4}} ight. \left \{ {{x=2} \atop {x=-2}} ight.; \left \{ {{x=5} \atop {y=5-4}} ight.\left \{ {{x=5} \atop {y=1}} ight.$ . В ответе будут две точки (2;-2) и (5;1). Ответ: $(2;-2); (5;1).$
- Автор:
  vivian
- 5 лет назад
- 0
Добавить свой ответ