-
отрицательная Функция кубического корня свойства ее ? ПЛИЗ ОЧЕНЬ НАДО
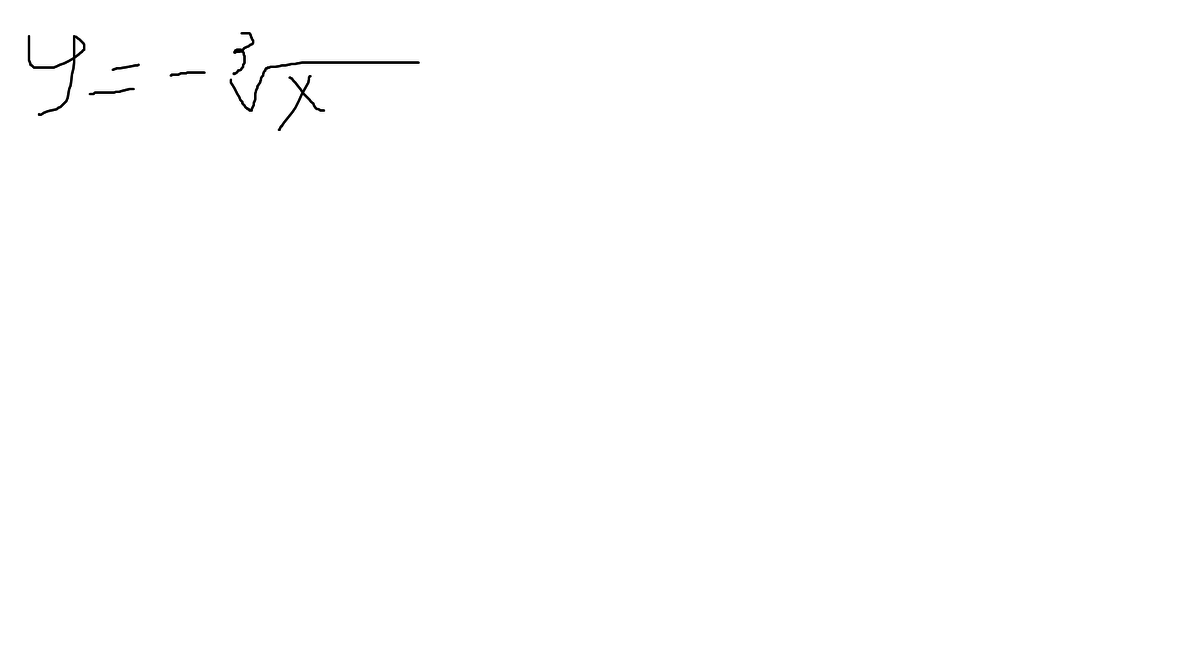
Ответы 5
-
В п.5 все в точности наоборот, выпуклый график вверх при х меньше нуля, а при х больше 0 - выпуклый вниз) рассматривал почему-то обычный корень)
-
Автор:
jadyn - 6 лет назад
-
0
-
-
а этот график точно для ОТРИЦАТЕЛЬНОГО графика ? :)
-
Автор:
katiexxgz - 6 лет назад
-
0
-
-
конечно, проверьте, если хотите :)
-
Автор:
kaiburke - 6 лет назад
-
0
-
-
спасибо )
-
Автор:
jethrocain - 6 лет назад
-
0
-
-
Итак, начала миниатюрного матана, вот они. Собственной персоной. У функции несколько свойств.1) D(f) или же dom f - область определения.2) R(f) или же ran f - область значений.3) Четность функции.4) Монотонность.5) Выпуклость (необязательно)6) Ограниченность ф-ии.7) Ну и последним будет периодичность (если есть).Остальное либо не уровень школы, либо не нужно.Собственно, для того, чтобы построить ф-ию нужны т.н. "асимптоты", которые найти мы с вами не сможем (вернее, сможем, но возникнет недопонимание между вами и вашем преподавателем).Ну и начнем.1) dom f = R, это очевидно, есть знать, что это, собственно, такое (даю краткую подсказку: область определение - множество, содержащее допустимые значения аргумента функции).2) ran f = R, вот тут сложнее (причем значительно), примем сие на веру (ну просто потому, что корень прямо пропорционален аргументу).3) Четная ли ф-ия? Посмотрим.Нечетная ф-ия: значит f(-x)=-f(x).
=
Это действительно так, поскольку (-n)^3=-n^3 , это свойство куба.Т.е. наша функция нечетная.4) Монотонность. Ну, если уровень 9-х классов, то, конечно, с ходу не определить (как и промежутки знакопостоянства, которые я опустил).Однако по графику можно увидеть - да мол, монотонно убывает на всем промежутке. Как раз из-за пропорциональности кубического корня :)5) Опустим (из-за невозможности строго определить). Но можно видеть, что при x<0 график явно выпуклый вниз, а при x>0 - вверх :)6) Собственно, ran f показал нам, что функция неограниченна. Посему так и пишем.7) Никакой периодичности тут нет (это можно видеть по графику, строго, опять же увы и ах, мы не сделаем).Вот такие свойства.Прикрепляю картинку графика :)

-
Автор:
jane94 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
помогите пожалуйста срочно! 106-x=92 с проверкой пожалуйста
-
Предмет:
Математика -
Автор:
molinabpjp - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Используя основное свойство дроби,найдите значение х:
7х-9/12=35/84-
Предмет:
Математика -
Автор:
grahammcdaniel - 6 лет назад
-
Ответов:
6 -
Смотреть
-
-
как упростить: 2(3-x)-(8+x)
-
Предмет:
Математика -
Автор:
leeblackwell - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Ножка, снежный, дорожка - одинаковая орфограмма ?
-
Предмет:
Русский язык -
Автор:
jacquelinewagner - 6 лет назад
-
Ответов:
3 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
