-
задания по теме "тригонометрия" помогите, чем сможете ЗАДАНИЕ ВО ВЛОЖЕНИИ
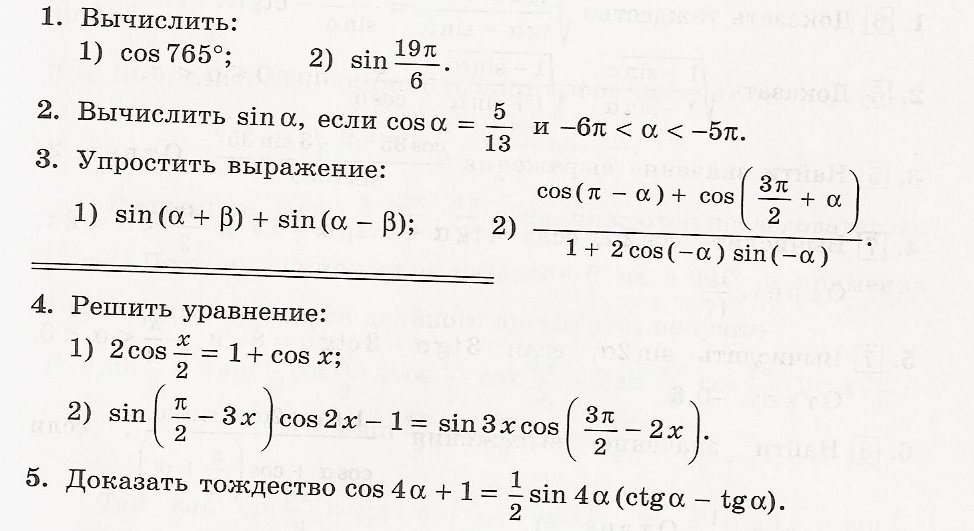
Ответы 1
-
1. 1) В таких случаях углы нужно приводить к сумме таких чисел, чтобы одно из слагаемых было кратно 90, а косинус другого слагаемого был табличным значением.765=720+45=360*2+45cos765=cos(360*8+45) - а это формула приведения
cos(360*2+45)=cos45=(корень из двух)\22)sin(19п\6)=sin(3п+п\6)=-sin(п\6)=-0,5
2. Здесь находится во основному тождеству (cosA)^2+(sinA)^2=1(sinA)^2=1-(cosA)^2(sinA)^2=1-25\169=144\169sinA=12\13 и
sinA=-12\13Но в задании сказано, что угол у тебя определен от -6п до -5п, а там синус положительный (кстати, в этом я немного сомневаюсь), значит подходит ответ 12\13 БЕЗ минуса3. 1) sin(a+b)+sin(a-b)=sin_a*cos_b+cos_a*sin_b+sin_a*cos_b-cos_a*sin_b=2sin_a*cos_b2) =(-cosA+sinA)\(1+2cosA*(-sinA))=(sinA-cosA)\(1-sin2A)Тут еще можно над знаменталем поработать, поделив числ. и зн. на 24. 1) Обе части в квадратИспользуется формула понижения степени4*(cos(x\2))^2=(1+cosx)^22+2cosx=1+2cosx+(cosx)^2(cosx)^2=1x=пn
2) =cos3x*cos2x-1=sin3x*(-sin2x)cos3x*cos2x+sin3x*sin2x=1cos(3x-2x)=1cosx=1x=2пn5. Чтобы доказать тождество, преобразуем правую часть:0,5sin4A*(cosA\sinA-sinA\cosA)=0.5sin4A*((cos^2A-sin^2A)\sinA*cosA)=0.5*2*cos2A*sin2A*(cos2A\sinA*cosA)=(cos2A)^2*2*cosA*sinA\sinAcosA=2(cos2A)^2=cos4A+1cos4A+1=cos4A+1ч.т.д.
-
Автор:
jaxsonbowman - 6 лет назад
-
0
-
-
Добавить свой ответ
-
рассказ дорога через лес из повести бунина в деревне
-
Предмет:
Русский язык -
Автор:
edgar40 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Детская площадка прямоугольной формы занимает площадь 225 квадратных м. Ширина площадки 9 м. Найди ее периметр.
-
Предмет:
Математика -
Автор:
chasityhatfield - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
тема спорт на эту тему нужно минимум 10 предложений 5 из них с причастиями и 5 с деепричастиями
-
Предмет:
Русский язык -
Автор:
hollyhiggins - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Напишите рецепт горячего бутерброда на английском.Пожалуйста.СРОЧНО!
-
Предмет:
Английский язык -
Автор:
hulkevls - 6 лет назад
-
Ответов:
2 -
Смотреть
-
