-
Решите, пожалуйста!
sqrt(3)sinx-sqrt(2sin^2x-sin2x+3cos^2x)=0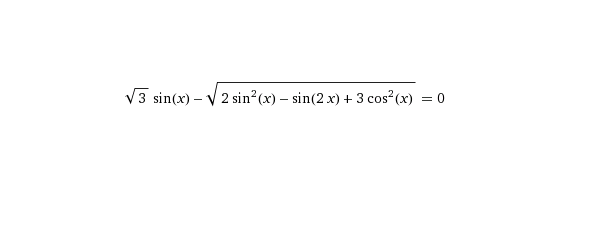
Ответы 4
-
Спасибо!
-
Автор:
juniormorrow - 6 лет назад
-
0
-
-
не за что)
-
Автор:
austinrvw9 - 6 лет назад
-
0
-
-
Можете помочь с остальными, пожалуйста? Хоть каким-либо из нихhttp://znanija.com/task/15884311http://znanija.com/task/15889086http://znanija.com/task/15889285http://znanija.com/task/15889441
-
Автор:
ashleer4u4 - 6 лет назад
-
0
-
-
переносим корень с синусами и косинусами в правую часть, тогда получается:sqrt(3)sinx=sqrt(2sin²x-sin2x+3cos²x)возводим обе части в квадрат, учитывая, что:2sin²x-sin2x+3cos²x>0решаем данное неравенство, приравниваем к 02sin²x-sin2x+3cos²x=0расписываем sin2x=2sinxcosx:2sin²x-2sinxcosx+3cos²x=0делим все на cos²x:2tg²x-tgx+3=0делаем замену, tgx=a2a²-a+3=0D=1-24=23<0 уравнение не имеет решений, решением неравенства будет являться вся вещественная ось, т.е. x∈(-∞;+∞)тогда получаем:3sin²x=2sin²x-sin2x+3cos²xпереносим все в левую часть:sin²x+sin2x-3cos²x=0представим sin2x как 2sinxcosx:sin²x+2sinxcosx-3cos²x=0делим все на cos²x:tg²x+2tgx-3=0делаем замену tgx=tt²+2t-3=0I I Ia b ck=b/2решаем квадратное уравнениеD1=k²-ac=1+3=4=2²t1=(-k+√D1)/a=-1+2=1t2=(-k-√D1)/a=-1-2=-3Обратная замена t=tgxtgx=1 tgx=-3x=π/4+πn, n∈Z x=arctg(-3)+πn, n∈ZОтвет:π/4+πn; arctg(-3)+πn, n∈Z
-
Автор:
halle - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Напишите сочинение про любого мальчика из рассказа " Бежин луг "
по плану:
1.Вступление
2.Из какой он семьи,его одежда
3.Его роль среди товарищей
4.История героя
5.Поведение мальчика
6.Отношение к ниму автора и ваше
ДАМ 20 БАЛЛОВ
-
Предмет:
Литература -
Автор:
brockwong - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
Найди лишнее и зачеркни знак, звук, запах, вкус
-
Предмет:
Информатика -
Автор:
weber - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
конструирование предложения. По, первая, пороша, охотники, пойти, на, охота.
-
Предмет:
Русский язык -
Автор:
susieoqtq - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
выбери слово ,которое является физической величиной:а)ветер, в)плотность, с)инерции, д)секунда , е)траектория.
-
Предмет:
Физика -
Автор:
biggiehkh4 - 6 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
