Задать вопрос Регистрация
Помочь другим

  • помогите пожалуйста найти контрольную работу с этим примером , ответ киньте в виде скрина или фото

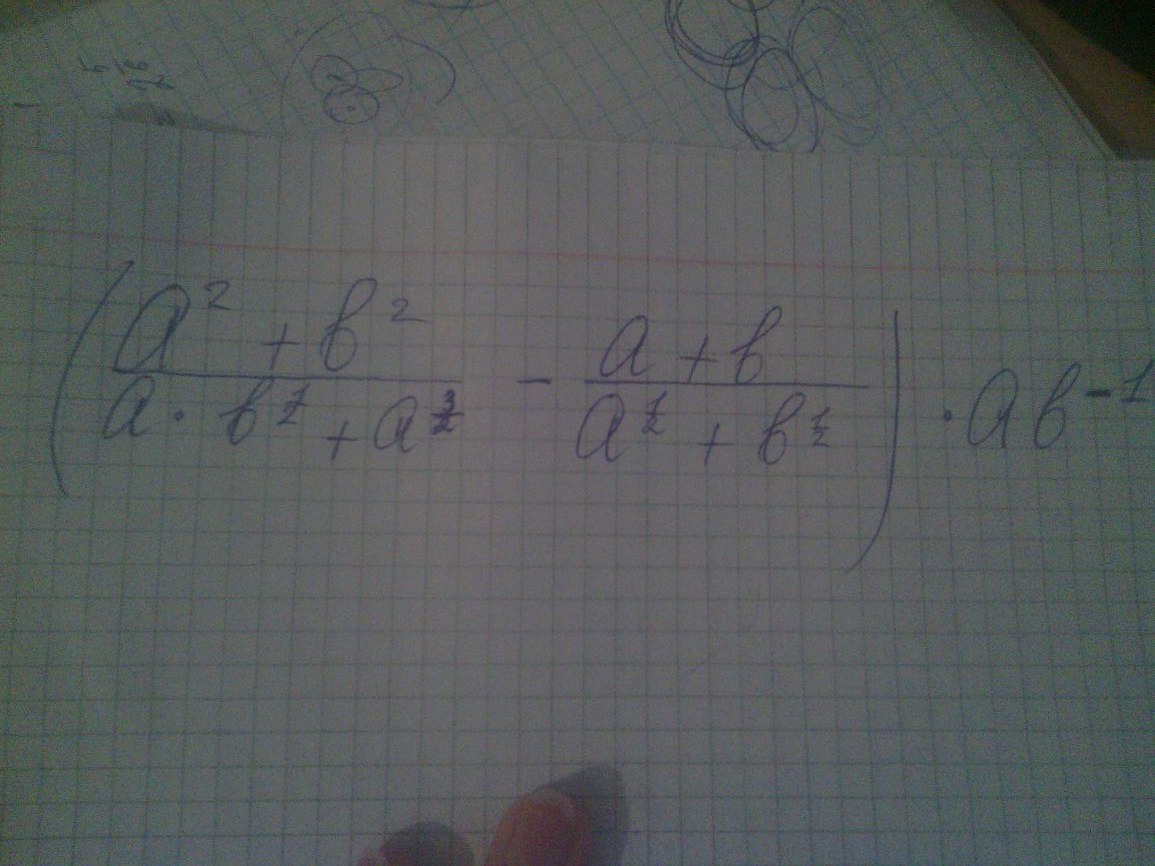
    question img

Ответы 1

  • (\frac{a^2+b^2}{ab^{\frac{1}{2}}+a^{\frac{3}{2}}}} - \frac{a+b}{a^{\frac{1}{2}}+b^{\frac{1}{2}}} )\cdot ab^{-1}=( \frac{a^2+b^2}{a(b^{\frac{1}{2}}+a^{\frac{1}{2}})} - \frac{a+b}{a^{\frac{1}{2}}+b^{\frac{1}{2}}} )\cdot \frac{a}{b}=\\\\= \frac{(a^2+b^2)(a^{\frac{1}{2}}+b^{\frac{1}{2}})-a(a+b)(b^{\frac{1}{2}}+a^{\frac{1}{2}})}{a(a^{\frac{1}{2}}+b^{\frac{1}{2}})^2}\cdot \frac{a}{b}= \frac{(a^{\frac{1}{2}}+b^{\frac{1}{2}})(a^2+b^2-a^2-ab)\cdot a}{a(a^{\frac{1}{2}}+b^{\frac{1}{2}})^2\cdot b} == \frac{b^2-ab}{b(a^{\frac{1}{2}}+b^{\frac{1}{2}})}= \frac{b(b-a)}{b(a^{\frac{1}{2}}+b^{\frac{1}{2}})} = \frac{(b^{\frac{1}{2}}-a^{\frac{1}{2}})(b^{\frac{1}{2}}+a^{\frac{1}{2}})}{a^{\frac{1}{2}}+b^{\frac{1}{2}}} =b^{\frac{1}{2}}-a^{\frac{1}{2}}

    • Автор:

      quinncain
    • 6 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years