-
Помогите решить пример из задачника Мордковича по алгебре за 8 класс 2013 года под номером 14.34 буква б. Избавиться от иррациональности в знаменателе. [tex]1/ \sqrt{2} + \sqrt{3} +1[/tex]. Файл прилагается. Заранее спасибо.
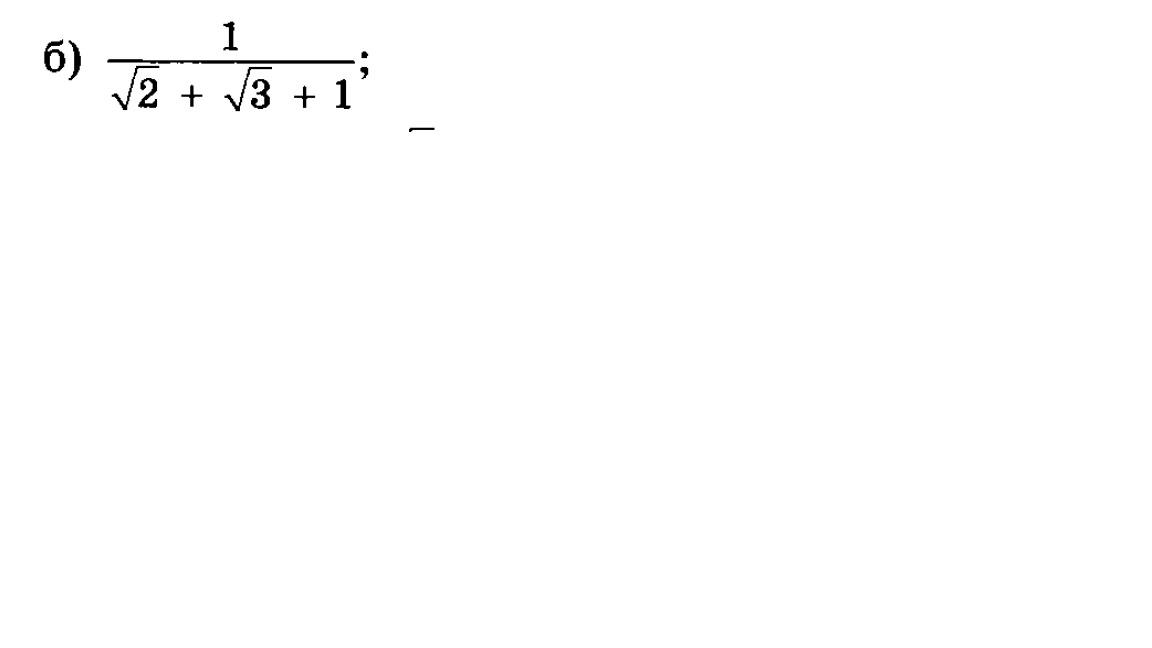
-
Предмет:
Алгебра -
Автор:
mischiefbazp - 6 лет назад
-
Ответы 6
-
и числитель и знаменатель домножили на (sqrt2+sqrt3-1), чтобы формулой воспользоваться (a-b)(a+b)
-
Автор:
ignacio83 - 6 лет назад
-
0
-
-
ответ в учебнике 2+sqrt2-sqrt6/4
-
Автор:
sexton - 6 лет назад
-
0
-
-
Раскрыть скобки в числителе надо
-
Автор:
cheesevtsn - 6 лет назад
-
0
-
-
Спасибо вам большое, не додумал, полный д*******.
-
Автор:
bodieh0nt - 6 лет назад
-
0
-
-
Дорешала до вида ответа
-
Автор:
seth - 6 лет назад
-
0
-
-
-
Автор:
elishavgvq - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- дать название веществу CuSO4
- Сообщение о Будде . Что привлекало последователей Будды в нём самом и его учении ? Как Будда относился к кастовым различиям между людьми ?
-
узнай о заповедниках,которые находятся на территории лесной зоны. Подготовьте сообщение об одном из них
-
Предмет:
Окружающий мир -
Автор:
nutmegherman - 6 лет назад
-
Ответов:
6 -
Смотреть
-
-
В магазине было 420 телевизоров, 1/7 всех телевизоров продали.На сколько меньше телевизоров продали, чем осталось?
-
Предмет:
Математика -
Автор:
lorenzoor6y - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
