-
На рисунке изображен график производной функции f(x), определенной на интервале (−10; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна y =x+1 или совпадает с ней.
С объяснением, пожалуйста.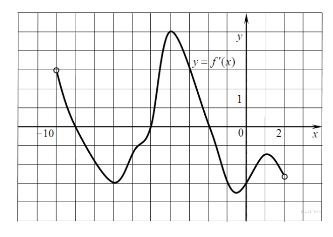
-
Предмет:
Алгебра -
Автор:
dariusvega - 5 лет назад
-
Ответы 1
-
Известно, что значение производной в точке есть угловой коэффициент касательной к графику функции в этой точке, то есть
Прямая у=х+1 имеет угловой коэффициент к=1 (коэффициент перед х). А параллельные прямые имеют равные угловые коэффициенты. Значит, на графике мы должны найти точки, в которых
Таких точек три, потому что график y=f'(x) пересекается с прямой у=1 в трёх точках.
-
Автор:
oscargibson - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Выберите правильный ответ:
1. К шляпочным грибам относится мухомор/головня
2. Грибы/лишайники изучает наука микология
3. Мукор размножается спорами/почкованием
4. На злаковых растениях паразитирует гриб трутовик/спорынья
5. Грибы могут размножаться почкованием/семенами
6. К ядовитым грибам относится пеницилл/бледная поганка-
Предмет:
Биология -
Автор:
chaneljohnston - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Сторона ромба равна 6 а острый угол равен 60 найти длину меньшей диагонали ромба -
на одном острове 2 миллиарда 345 на другом два миллиарда триста 45 человек Сколько человек на двух островах вместе
-
Предмет:
Математика -
Автор:
emanuel - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
найдите значение вырожение 3.6 черта дроби 0.45
-
Предмет:
Математика -
Автор:
javion - 5 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
