-
Решите логарифмическое уравнение! Буду очень признательна. Плоховасто видно, поэтому запишу таким образом:
log^2 0.5(x-5)+log 2(4/x-5)=(3/5)^log 3/5 1/4+ log 3/5 8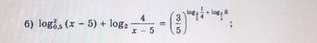
Ответы 6
-
А если приводить к основанию 2, а не 1/2? Получится такой же ответ?
-
Автор:
aurelio - 6 лет назад
-
0
-
-
да
-
Автор:
collinvasquez - 6 лет назад
-
0
-
-
У меня почему-то не сходится. Посмотрите, пожалуйста2. log2(x-5)=-1log2(x-5)=log2(1/2)x-5=1/2
-
Автор:
natividad0oat - 6 лет назад
-
0
-
-
В самом решении написан второй способ при основании 2.
-
Автор:
shane35 - 6 лет назад
-
0
-
-
Большое спасибо )
-
Автор:
garrett - 6 лет назад
-
0
-
-
ОДЗ:x-5>0x>5
1)
2)
2 способ:
1)
2)
Ответ: 6; 7.
-
Автор:
oakley13 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
прочетайте слова. запишите их в три столбика. односложные,двусложные и трехсложные. группа,касса,килограмм,шоссе,аллея,колонна,пассажир,жужжание,ванна,класс,сумма,троллейбус,аппетит,суббота,ссора,бассейн,антенна,грипп.
-
Предмет:
Русский язык -
Автор:
bubblesblack - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Пставте пропущенных буквы.
Выход... те на крыльцо.
Влажный ветерок изредка... набега... ты лёгкой волной.
Телега громким... застучала.
Ед... те с горы направ...
Вам холодн... немножк... вы закрыва... те лицо
Светле... ты воздух, ясне... т небо-
Предмет:
Русский язык -
Автор:
autumn50 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
- нарисуйте схему цепи карманного фонаря и назовите части этой цепи. какие элементы фонаря отмечены цифрами
-
составить предложение со словом енот
-
Предмет:
Русский язык -
Автор:
remy6e6f - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
