Задать вопрос Регистрация
Помочь другим

  • Вычислите производные следующих функций. В каждом случае указать правила

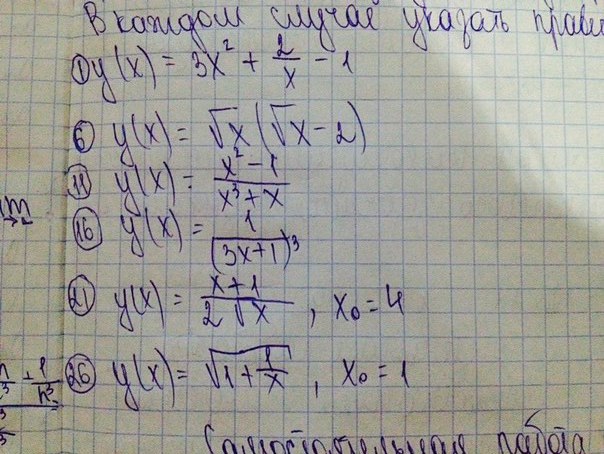
    question img

Ответы 1

  • y(x) = 3 x^{2} + \frac{2}{x} -1Правило: ( x^{n})' = nx^{n-1} y' = 6x- \frac{2}{x^{2}}y(x) =√x·(√x-2) = x - 2√xПравило: (\sqrt{x})' = \frac{1}{2 \sqrt{x} } y'(x) = 1-\frac{1}{ \sqrt{x}}y(x) = \frac{ x^{2} -1}{x^{3} +x} Правило: ( \frac{u}{v} )'= \frac{u'*v-u*v'}{v^{2} } y'(x) = \frac{2x*( x^{3}+x)-( x^{2} -1)(3 x^{2} +1) }{ (x^{3}+x)^{2} } = \frac{2x^{4}+2x^{2} -3x^{4}-x^{2} +3x^{2}+1 }{ (x^{3}+x)^{2} }=\frac{-x^{4}+4x^{2}+1 }{ (x^{3}+x)^{2} } y(x) = \frac{1}{(3x+1)^{3}} =(3x+1)^{-3} Правило: g'[f(x)] = g'_{f}*f'_{x} y'(x) = -3·(3x+1)⁻⁴·3 = -\frac{9}{(3x+1)^{4} } y(x)= \frac{x+1}{2 \sqrt{x} } , x₀ = 4 Правило: ( \frac{u}{v} )'= \frac{u'*v-u*v'}{v^{2} } y'(x) = \frac{2 \sqrt{x} -(x+1) \frac{1}{ \sqrt{x}} }{4x} = \frac{2x-x-1}{4x \sqrt{x} }=\frac{x-1}{4x \sqrt{x} } y'(x_{0}) = y'(4) = \frac{4-1}{4*4* \sqrt{4} } = \frac{3}{32} y(x) = \sqrt{1+ \frac{1}{x} }, x_{0} =1Правило: g'[f(x)] = g'_{f}*f'_{x} y'(x)= \frac{-\frac{1}{ x^{2}} }{2 \sqrt{1+ \frac{1}{x} } } =- \frac{1}{2 x^{2}*\sqrt{1+ \frac{1}{x} } } y'(x_{0})=y'(1)==- \frac{1}{2*1^{2}*\sqrt{1+ \frac{1}{1} } } =- \frac{1}{2 \sqrt{2} }

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years