-
Решить иррациональное уравнение, нужна ваша помощь.
Номера ввиде фотографий.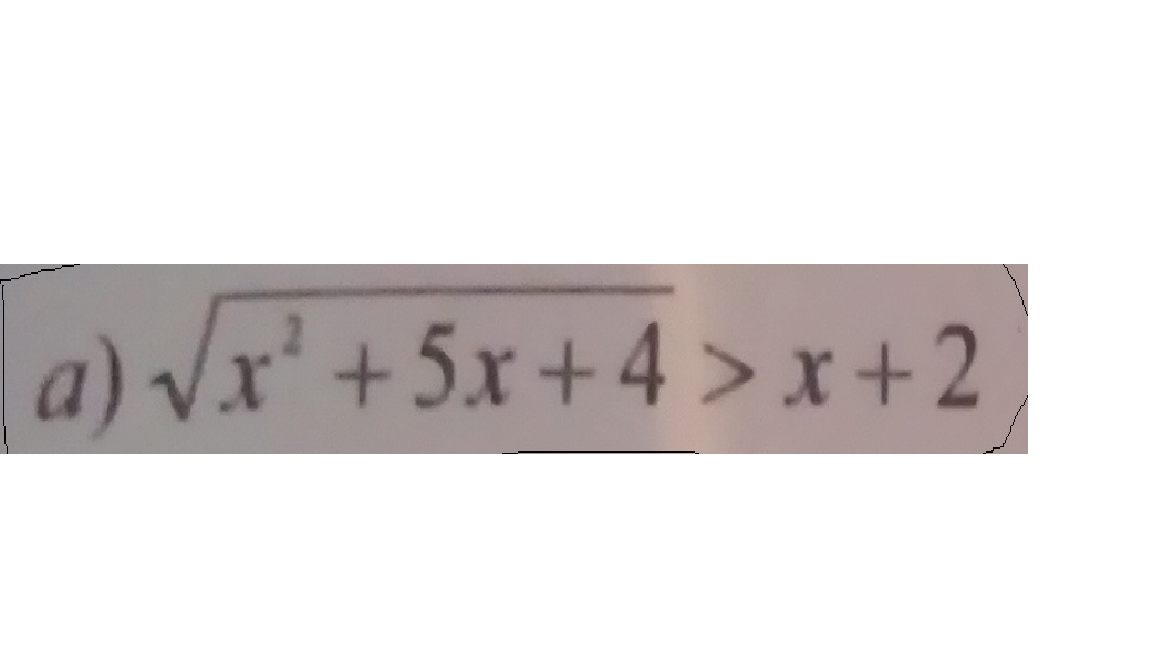

Ответы 4
-
Это было пример под буквой a, не могли бы вы решить и под буквой b?
-
Автор:
dotsf6l0 - 6 лет назад
-
0
-
-
b) решен
-
Автор:
leilani - 6 лет назад
-
0
-
-
Благодарю вас!
-
Автор:
abrahán6fzu - 6 лет назад
-
0
-
-
a)
Рассматриваем две системы неравенств:
1)a) x+2<0 x< -2b) x²+5x+4≥0D=25-16=9x₁=(-5-3)/2=-4x₂=(-5+3)/2=-1\\\\\\\\\\\\\\\\\\\\\\\-------- -4 ------- -2 ------- -1 -----------\\\ + \\\\\ \\\\+\\\\\\\\x∈(-∞; -4]2)a) x+2≥0 x≥ -2b) x²+5x+4>(x+2)² x²+5x+4>x²+4x+4 x²-x²+5x-4x>4-4 x>0 \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\--------- -2 ---------- 0 ----------------- \\\\\\\\\\\\\\\\\\\\x∈(0; +∞)В итоге x∈(-∞; -4]U(0; +∞)b)
Система неравенств:{x+2≥0{3x²+5x-2≤(x+2)²{3x²+5x-2≥0a) x+2≥0 x≥ -2b) 3x²+5x-2 ≤ (x+2)² 3x² +5x-2 ≤ x² +4x+4 3x² - x²+5x-4x-2-4 ≤ 0 2x² +x -6 ≤ 0 D=1+48=49 x₁=(-1-7)/4= -2 x₂=(-1+7)/4=1.5 + - +--------- -2 ----------- 1.5 -------------- \\\\\\\\\\\\\\x∈[-2; 1.5]c) 3x²+5x-2≥0 D=25+24=49 x₁=(-5-7)/6= -2 x₂=(-5+7)/6=2/6=1/3 + - +------- -2 ------------ 1/3 ----------------\\\\\\\\\ \\\\\\\\\\\\\\\\\x∈(-∞; -2]U[1/3; +∞){x≥ -2{x∈[-2; 1.5]{x∈(-∞; -2]U[1/3; +∞) \\\\\\\\\\\\\\\\\\\\\\\\\\\\------ -2 --------- 1/3 -------- 1.5 -------------/////// //////////////////////////////////x∈[1/3; 1.5]Ответ: [1/3; 1.5]
-
Автор:
rodgers - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
подчеркните подлежащее и сказуемое
Равнины белеют под снегом,чернится лес.-
Предмет:
Русский язык -
Автор:
bandittseb - 6 лет назад
-
Ответов:
5 -
Смотреть
-
- покажите на карте крупные озера моря и реки земного шара
-
как встретились жилин и костылин ? как они себя вели в плену? почему Дина помогла жилину ? что хочет сказать нам писатель, рассказывая об этой дружбе? почему не удался первый побег? как относились к жилину татары. в чём смысл рассказа? что осуждает писатель ( бессмысленность вражды между народами, бессмысленность войны или что-то другое)?
-
Предмет:
Литература -
Автор:
colin3ycl - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
как решить пример 875 : 125 прошу помогите
-
Предмет:
Математика -
Автор:
jonathanpaig - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
