Решите систему уравнений
1. х-4у=3
ху+2у=9
2. х*2+6ху+9у*2=16
х-3у=-2
Решите задачу
Площадь прямоугольника равна 300см*2. Если его длину увеличить на 5 см,а ширину уменьшить на 5 см,то его площадь будет равна 250 см*2. Найти начальные размеры прямоугольника
Решите графически систему уравнений
у=х*2 -4х
х-у=6

Ответ:

1)

(7; 1)

2)

(1;\ 1)

\Big(-3;\ -\dfrac{1}{3}\Big)

3)

а = 20 см

b = 15 см

4)

(2; - 4)  (3; - 3)

Объяснение:

1.

\left\{ \begin{array}{ll}x-4y=3\\xy+2y=9\end{array}

\left\{ \begin{array}{ll}x=4y+3\\(4y+3)y+2y=9\ \ \ \ \ \ (1)\end{array}

1)

(4y+3)y+2y=9

4y^{2}+3y+2y-9=0

4y^{2}+5y-9=0

D=25+144=169=13^{2}

y_{1}=\dfrac{-5-13}{8}=-\dfrac{9}{4}

y_{2}=\dfrac{-5+13}{8}=1

\left\{ \begin{array}{ll}x=4y+3\\y=-\dfrac{9}{4}\end{array}      \left\{ \begin{array}{ll}x=4y+3\\y=1\end{array}

\left\{ \begin{array}{ll}x=-6\\y=-\dfrac{9}{4}\end{array}           \left\{ \begin{array}{ll}x=7\\y=1\end{array}

\Big(-6;\ -\dfrac{9}{4}\Big)

(7;\ 1)

_________________

2.

\left\{ \begin{array}{ll}x^{2}+6xy+9y^{2}=16\\x-3y=-2\end{array}

\left\{ \begin{array}{ll}(x+3y)^{2}=16\\x-3y=-2\end{array}

\left[\begin{array}{ll}\left\{ \begin{array}{ll}x+3y=4\\x-3y=-2\end{array}\\\left\{ \begin{array}{ll}x+3y=-4\\x-3y=-2\end{array}\end{array}

\left[\begin{array}{ll}\left\{ \begin{array}{ll}2x=2\\x-3y=-2\end{array}\\ \left\{ \begin{array}{ll}2x=-6\\x-3y=-2\end{array}\end{array}

\left[\begin{array}{ll}\left\{ \begin{array}{ll}x=1\\y=\dfrac{x+2}{3}\end{array}\\\left\{ \begin{array}{ll}x=-3\\ y=\dfrac{x+2}{3}\end{array}\end{array}

\left[\begin{array}{ll}\left\{ \begin{array}{ll}x=1\\y=1\end{array}\\\left\{ \begin{array}{ll}x=-3\\ y=-\dfrac{1}{3}\end{array}\end{array}

(1;\ 1)

\Big(-3;\ -\dfrac{1}{3}\Big)

___________________

3.

a - длина прямоугольника,

b - ширина прямоугольника,

ab - площадь прямоугольника.

а + 5 - новая длина прямоугольника,

b - 5 - новая ширина прямоугольника,

(a + 5)(b - 5) - новая площадь.

\left \{ \begin{array}{ll}ab=300\\(a+5)(b-5)=250\end{array}

\left \{ \begin{array}{ll}ab=300\\ab-5a+5b-25-250=0\end{array}

\left \{ \begin{array}{ll}ab=300\\300-5a+5b-275=0\end{array}

\left \{ \begin{array}{ll}ab=300\\5a-5b=25\end{array}

\left \{ \begin{array}{ll}ab=300\\a-b=5\end{array}

\left \{ \begin{array}{ll}a=b+5\\(b+5)b=300\ \ \ \ (1)\end{array}

1)\ b^{2}+5b-300=0

D=25+1200=1225=35^{2}

b=\dfrac{-5-35}{2}=-20 - не подходит по смыслу

b=\dfrac{-5+35}{2}=15

\left \{ \begin{array}{ll}b=15\\a=20\end{array}

а = 20 см

b = 15 см

__________________

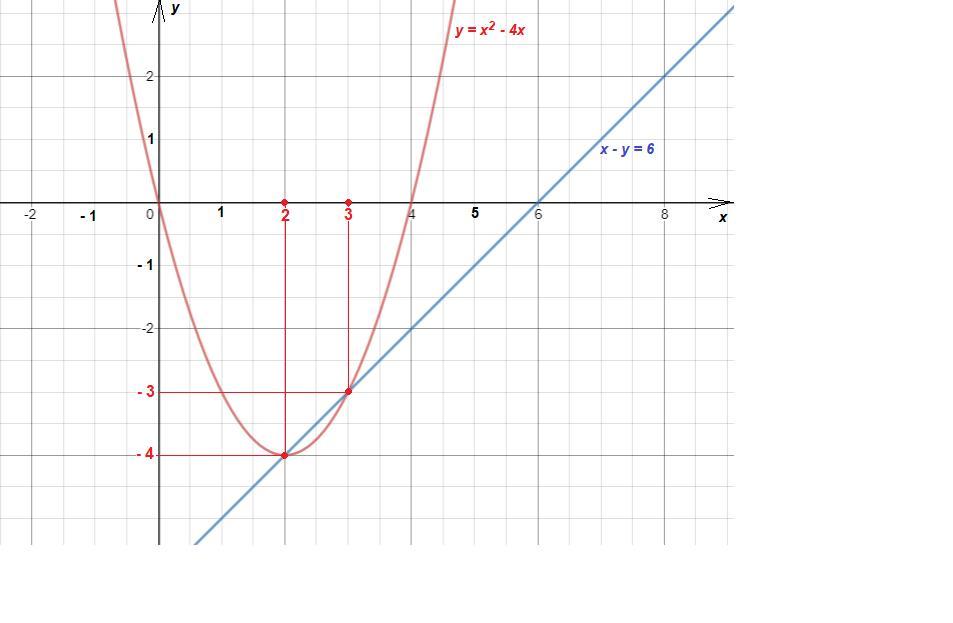
4.

\left \{ \begin{array}{ll}y=x^{2}-4x\\x-y=6\end{array}

1) y = x² - 4x

Функция квадратичная, график - парабола, ветви направлены вверх.

Координаты вершины:

x_{0}=-\dfrac{b}{2a}=\dfrac{4}{2}=2

y(2) = 2² - 4 · 2 = 4 - 8 = - 4

(2; - 4)

Нули:

x² - 4x = 0

x(x - 4) = 0

x = 0   или   х = 4.

График красный.

2) x - y = 6

y = x - 6

Функция линейная, график - прямая.

Находим координаты двух точек:

(0; - 6)    (6; 0)

Синий график.

Координаты точек пересечения и есть решения системы уравнений:

(2; - 4)  (3; - 3)